Travaillant dans des pays différents, les auteurs de cet article lancent un célèbre logiciel de vidéoconférence qu’ils ne citeront pas. Sur leurs écrans respectifs s’affichent des endroits séparés de plus de 600 km. Microphones et hauts-parleurs transforment leurs paroles en courants électriques, qui traversent l’Europe à la vitesse de l’éclair. D’un bout à l’autre, nous trouvons des ondes. Les plus familières, celles que nous voyons et entendons tous les jours, sont les ondes lumineuses et sonores. Le long des fils de cuivre, ce sont aussi des ondes — électroniques cette fois — qui transportent l’information, parfois relayées par des ondes lumineuses le long de fibres optiques. D’un routeur à nos ordinateurs portables, des ondes électromagnétiques, sœurs des ondes lumineuses, forment la trame du wifi qui nous permet de communiquer. La physique des ondes unifie tous ces phénomènes en les décrivant — mathématiquement — de la même façon.
Comme les ondes sont notre principal (sinon seul) moyen de transmettre de l’information, contrôler leur propagation est un enjeu à la fois fondamental et technologique — qu’il s’agisse de l’améliorer ou au contraire de s’en protéger. Une des méthodes pour y parvenir consiste à utiliser des métamatériaux. La propagation des ondes dans un matériau est drastiquement modifiée par l’existence d’une structure à l’échelle de la longueur d’onde. En disposant des éléments de manière régulière dans l’espace, à une échelle comparable aux longueurs d’onde en jeu, il est possible de réaliser des milieux aux propriétés particulières, totalement différentes de celles qu’aurait un bloc du matériau dans lequel les blocs de base sont construits. C’est ainsi que l’évolution a doté certains papillons, comme le Parides sesostris de la figure 1, d’une intense coloration structurelle métallique : leurs ailes sont organisées à l’échelle nanométrique pour former un cristal photonique, dans lequel la lumière verte ne peut pas pénétrer. Elle est donc réfléchie, ce qui donne sa couleur caractéristique à l’aile. En plus de donner couleur à certains papillons, les métamatériaux permettent de fabriquer des objets aux propriétés fascinantes [3] [4]: des « capes d’invisibilité », des lentilles à indice de réfraction négatif, ou encore des guides d’ondes à sens unique.

L’espace dans lequel nous vivons se comporte de la même façon dans toutes les directions. Ainsi la lumière d’une lampe se propage aussi bien vers la droite que vers la gauche, vers le haut que vers le bas, etc. Dans certains systèmes comme les fibres optiques, on peut certes confiner la lumière dans une seule direction, [5] mais la propagation dans les deux sens est toujours possible le long de cette direction. Il est donc difficile d’imaginer comment peut bien se comporter un guide d’onde à sens unique ! Sur une route à sens unique, il est physiquement possible de rouler dans les deux sensa. Dans un guide d’onde unidirectionnel, au contraire, la propagation de la lumière est tout simplement impossible dans un sens, du moins pour certaines couleurs.
Comment réaliser un tel objet ? La solution consiste à séparer spatialement les deux sens de propagation par un (méta)matériau aux propriétés très particulières : un isolant topologique. Dans un tel système, la propagation de la lumière aux fréquences qui nous intéressent est interdite, comme la lumière verte dans les ailes du papillon Parides sesostris. Cette contrainte permet l’existence de différentes classes de matériaux qui diffèrent par la structure interne des ondes qu’ils supportent, et en particulier par leur topologie (nous préciserons ce que cela signifie sous peu). Notre guide d’onde à sens unique est en fait constitué par l’interface entre deux de ces matériaux.
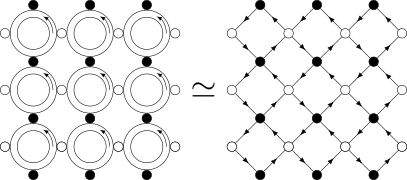
Ici, les briques élémentaires qui composent le métamatériau sont des résonateurs circulairesb où on peut considérer que la propagation de la lumière est confinée le long d’une sorte de fibre optique en anneau. Dans un tel système, la lumière peut se propager dans les deux sens, mais les deux sens de propagation sont découplés : si on envoie une onde lumineuse dans un sens, elle continuera à tourner dans ce sens indéfiniment. Lorsque de tels résonateurs sont placés les uns à côté des autres, une partie de la lumière peut passer de l’un à l’autre, comme on le voit sur les figures 2 et 3. Une ligne de résonateurs ainsi couplés forme un guide d’onde, que les opticiens appellent affectueusement CROWc [6] [7], mais ce genre de guide d’onde n’a rien d’unidirectionnel ! Cependant, nous allons voir qu’en assemblant les mêmes briques de manière astucieuse dans un plan [8], il est possible de réaliser un métamatériau qui interdit la propagation de certaines couleurs en son sein, et au bord duquel un guide d’onde unidirectionnel apparaît.
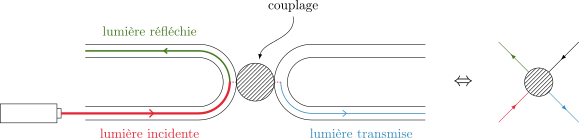
Décrire exactement la propagation de la lumière dans un tel matériau est en général très compliqué. Pour comprendre ce qu’il s’y passe, il est commode de simplifier autant que possible. Notre approche consiste à remplacer chaque connexion entre deux résonateurs par un nœud qui décrit comment la lumière est réfléchie et transmise d’un résonateur à l’autre (voir figure 2). Ces nœuds sont reliés par des flèches qui représentent les résonateurs ! Le métamatériau est ainsi remplacé par un graphe appelé un « réseau orienté », dans lequel la lumière se propage de manière discrète, à la fois dans l’espace et le temps (voir figure 3). Retenons simplement qu’à chaque étape, (i) la lumière se propage dans un seul sens le long des flèches et (ii) chaque nœud du réseau redistribue la lumière venant des flèches entrante vers les flèches sortantes, en conservant la quantité totale de lumière.
Même si la lumière se propage dans un seul sens le long des flèches, la lumière peut se propager dans toutes les directions à l’intérieur du réseau (voir figure 3). Il n’en est pas de même au bord ! Pour comprendre pourquoi, nous devons faire un plongeon dans la topologie algébrique, une branche des mathématiques qui s’occupe de la forme des objets.
En mathématiques, la topologie s’intéresse à la forme globale des objets et ignore leurs tailles et leurs petits détails. Par exemple, un beignet et une tasse ont la même topologie : on peut déformer continûment l’un en l’autre, car ils ont tous les deux un et un seul trou. Ils n’ont en revanche pas la même topologie qu’une orange, qu’il faudrait percer brutalement pour obtenir un beignetd. En physique, une quantité topologique est la même pour deux modèles que l’on peut continûment déformer l’un en l’autre, en respectant certaines conditions. Par analogie, imaginons que le beignet et la tasse soient deux modèles physiques. Enroulons un fil autour du beignet et considérons le nombre de tours que fait ce fil. Il est impossible de changer ce nombre sans couper le fil (ou le beignet), et même si l’on déforme le beignet en une tasse, le nombre de tour que fait le fil autour de l’anse de la tasse restera le même : c’est bien une quantité topologique.

Revenons maintenant aux métamatériaux : dans le graphe qui représente le système, les nœuds représentent les couplages entre résonateurs. À chaque nœud, la lumière sortant d’un résonateur est partiellement transmise à ses voisins, et partiellement réfléchie dans le résonateur initial, ce qu’on représente par des flèches qui pointent vers le nœud (pour la lumière « entrante ») ou en partent (pour la lumière « sortante »). La propagation de la lumière dans un tel réseau orienté est entièrement décrite par une fonction notée U qui détermine la lumière sortant de chaque nœud à partir de la lumière entrant dans chaque nœude.
Considérons d’abord la configuration la plus simple, où tous les résonateurs sont déconnectés (figure 5). La lumière ne fait alors que tourner dans chaque résonateur, comme le hamster proverbial ! Notons la fonction U correspondante U↺. Dans le cas extrême opposé, où toute la lumière d’un résonateur est transmise au suivant, on constate en suivant son chemin que la lumière est emprisonnée entre quatre résonateurs, et tourne dans le sens opposé (figure 5). Appelons la fonction correspondante U↻. Dans les deux cas, on constate que la lumière ne se propage pas dans le matériau : si on envoie de la lumière dans un résonateur, elle reste confinée dans celui-ci ou dans ses proches voisins. Il s’agit de la même situation que dans les ailes du papillon, où la lumière verte ne peut pas se propager.
Notre travail [9] a consisté à démontrer que cette absence de propagation est reliée à une quantité topologique. Ainsi nous avons construit une quantité W(U) qui détermine comment la lumière est piégée. On a par exemple W(U↺) = +1 alors que W(U↻) = -1. Ici, une lectrice perspicace pourrait commencer à soupçonner les auteurs d’avoir donné un nom pompeux à une chose évidente, à savoir le sens dans lequel tourne la lumière. Mais cette interprétation n’est évidente que dans les deux situations extrêmes de la figure 5 ! Comme W(U) est une quantité topologique, elle ne change pas lorsque l’on déforme un peu le système. Par exemple si la lumière est transmise à 90 % d’un résonateur au suivant et que 10% est réfléchie dans le résonateur initial, on aura toujours strictement W(U) = −1, et pas −0.9. Dans ce cas pourtant, une partie de la lumière fuite de proche en proche dans les résonateurs voisins et semble se propager dans le matériau. Cependant, la quantité de lumière qui se propage est de plus en plus infime, si bien que globalement la majeure partie s’accumule autour de la trajectoire circulaire initiale: elle reste ainsi piégée, et c’est précisément ce que décrit W(U).
On continue donc à avoir W(U) = -1 même lorsqu’on diminue progressivement la quantité de lumière transmise dans le résonateur suivant, jusqu’au moment où la quantité de lumière transmise est égale à la quantité de lumière réfléchie. À ce moment (et à ce moment seulement), la lumière peut se propager dans tout le système, et la grandeur W(U) n’est plus définie ! C’est ce qui lui permet de changer de valeur : quand la lumière est plus réfléchie que transmise, W(U) = +1 et la lumière est globalement piégée autour de la trajectoire qui tourne dans l’autre sens.
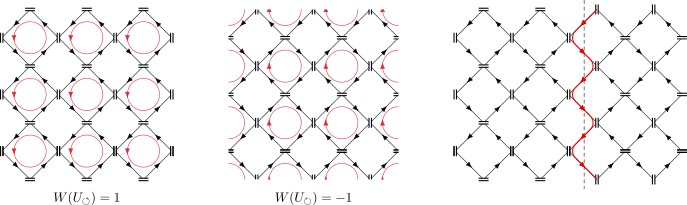
Résumons : chaque fonction U décrit une configuration physique (une tasse) et W(U) est une quantité topologique associée (un nombre de tour de fils). Il existe une infinité de U possibles où la lumière reste piégée, mais il n’y a que deux configurations topologiquement distinctes, chaque U pouvant être continûment déformée en U↺ ou bien en U↻. Considérons maintenant un système où l’on colle ensemble deux réseaux, l’un avec W = +1 et l’autre avec W = −1 . Nous avons vu que le seul moyen de changer de valeur de W en modifiant le matériau consiste à autoriser la propagation de la lumière. À l’interface entre les deux systèmes, tout se passe comme si l’on avait une succession de matériaux différents, qui relient les deux côtés de manière continue. Par conséquent, il faut autoriser la propagation de la lumière quelque part entre les deux matériaux. Ainsi, la lumière se propage forcément au niveau de la jonction ! On peut s’en convaincre en observant l’interface entre les deux cas extrêmes mentionnés précédemment (figure 5). On observe aussi que la lumière se propage dans un seul sens à l’interface. La propagation dans l’autre sens est strictement impossible. Dans le matériau de part et d’autre de l’interface, toute propagation est impossible, si bien qu’il ne reste qu’un guide d’onde unidirectionnel à l’interface.
Comme ce guide d’onde apparaît grâce aux propriétés topologiques des métamatériaux, on dit que son existence est « protégée topologiquement ». Même lorsque les connexions entre les résonateurs ne sont pas parfaites dans le matériau, il est toujours présent. Cette protection couvre aussi le caractère unidirectionnel du guide. Dans un guide d’onde habituel, comme une fibre optique, la présence d’un défaut provoque une réflexion partielle de la lumière sur le défaut (figure 6). Dans notre cas, il n’est tout simplement pas possible de réfléchir la lumière, puisqu’elle ne peut se propager que dans un sens. Par conséquent, la lumière contourne simplement le défaut et est entièrement transmise !

Grâce aux métamatériaux et leurs propriétés topologiques, on peut ainsi transmettre parfaitement la lumière le long d’une interface. Notons enfin que cette histoire est valable pour n’importe quelle onde (sonore, électronique, etc.), pour peu que l’on arrive à construire le métamatériau adéquat. Nous avons pris l’exemple de lumière, mais la même histoire pourrait être écrite avec un autre acteur comme premier rôle.
Quelques remarques pour aller plus loin
-
L’idée d’utiliser des résonateurs couplés (CROW) pour réaliser des systèmes topologiques en optique a été proposée (et réalisée) par M. Hafezi, E. Demler, M. Lukin, et J. Taylor [8]. Plusieurs articles de Y. Chong, G. Liang et M. Pasek [10] [11] ont contribué à la compréhension théorique de cette méthode en décrivant les systèmes étudiés par des réseaux orientés inspirés de travaux de J. Chalker, P. Coddington et C.-M. Ho [12] [13] datant des années 1990 sur l’effet Hall quantique, et en proposant un lien avec des systèmes sous forçage périodique dans le temps (appelés « de Floquet »). Un équivalent acoustique a été réalisé par Y.-G. Peng et al [14], et un système similaire a été proposé par A. Khanikaev, R. Fleury, S. Mousavi et A. Alù [15].
-
Comme on le voit sur la figure 3, le couplage entre résonateurs préserve le sens de rotation de la lumière. En fait, physiquement, c’est exactement le contraire qui se passe : lorsque deux résonateurs sont proches l’un de l’autre, ils sont couplés par des ondes évanescentes. Une onde tournant dans le sens horaire dans un résonateur est couplée à une onde tournant dans le sens anti-horaire dans l’autre résonateur, et ce couplage horaire—anti-horaire est très bien vérifié. Dans la figure 3, les petits coupleurs noirs et blancs sont en fait eux-mêmes des résonateurs en anneau. Lorsque des couplages horaire/horaire et anti-horaire/anti-horaire existent au niveau microscopique, par exemple à cause de défauts à l’intérieur d’un résonateur, la description que nous avons présentée ici n’est plus suffisante, et il faut prendre en compte tous les degrés de liberté (avec un réseau plus compliqué). Les propriétés topologiques ne sont pas préservées par de tels défauts. S’il n’y en a que quelques-uns, ça n’est pas un gros problème. Par contre, s’il y en a beaucoup, les propriétés topologiques n’ont plus vraiment de sens.
-
La propagation des ondes satisfait généralement une symétrie particulière, appelée réciprocité, qui signifie essentiellement que lorsque la propagation des ondes est possible d’un objet à un observateur, une onde peut aussi se propager de l’observateur à l’objet. À strictement parler, un guide d’onde à sens unique est un système qui n’est pas réciproque. Mais la réciprocité est une propriété très robuste, dont il n’est pas facile de se débarrasser. Plus précisément, un système linéaire invariant par renversement du temps et sans dissipation est forcément réciproque [16]. La description que l’on a donnée pourrait faire croire que la réciprocité est supprimée sans briser l’invariance par renversement du temps, ni non-linéarité, ni dissipation, mais ça n’est bien entendu pas vrai. En effet, la description complète du système physique doit inclure d’une part les deux sens de rotation dans chaque résonateur, et d’autre part prendre en compte la taille finie du système, et donc l’existence d’autre interfaces (avec leurs états de bord). La réciprocité est alors vérifiée.
-
Il y a une différence fondamentale entre les états de bord unidirectionnels liés à des isolants topologiques et, disons, une diode ou un isolateur optique utilisant l’effet Faraday. Ces derniers sont des éléments non-réciproques, qui peuvent donner l’impression de réaliser un guide d’onde à sens unique. Mais ça n’est pas le cas : ils ne font que se débarrasser d’un des sens de propagation, en le dissipant à l’endroit où ils se trouvent. Au contraire, au sein d’un état de bord unidirectionnel, la propagation dans un sens est interdite (dans le sens où elle est physiquement impossible) en chaque point ! Il s’agit d’une propriété complètement différente, qui confère au système topologique une grande robustesse vis-à-vis des défauts, ne le rend pas pour autant non-réciproque (voir la remarque 3). Un véritable guide d’onde à sens unique, que nous ne décrivons pas ici, nécessite à la fois des effets topologiques et des éléments non-réciproques.
-
Nous choisissons d’appeler « métamatériaux » tous les systèmes structurés à une échelle mésoscopique, relativement grande devant les échelles moléculaires. Il est néanmoins utile d’indiquer la distinction que certains font entre les cristaux photoniques, phononiques, acoustiques, etc. où l’échelle de longueur caractéristique est de l’ordre de la longueur d’onde en jeu, et les « métamatériaux » au sens strict, où l’échelle de longueur caractéristique est beaucoup plus petite que la longueur d’onde. En conséquence, les métamatériaux au sens strict sont généralement décrits par des « propriétés effectives », ce qui n’est jamais suffisant pour les cristaux photoniques. La distinction n’est toutefois pas toujours aussi évidente [17], et nous utilisons « métamatériaux » dans les deux cas.
Notes
| a. | ↑ | Nous déconseillons toutefois de réaliser l’expérience. |
| b. | ↑ | Vers la fin des années 1880, Lord Rayleigh donne une première description théorique des « Whispering Gallery modes », des modes acoustiques que l’on peut observer dans les galeries des murmures comme celle de la cathédrale Saint-Paul de Londres. Ces galeries tirent leur nom de leurs propriétés acoustiques particulières : un murmure prononcé, face au mur, d’un côté de la galerie est entendu clairement de l’autre côté, à plusieurs dizaines de mètres de distance, car le son est guidé le long de la courbe du mur ! Ces modes de galerie se retrouvent aussi à plus petite échelle, tant pour le son ou la lumière que d’autres ondes. |
| c. | ↑ | Pour Coupled Resonator Optical Waveguides. L’analogue acoustique s’appelle CRAW. |
| d. | ↑ | Les mathématiciens ne sont pas toujours bons cuisiniers. |
| e. | ↑ | Pour être plus précis, U est une application linéaire unitaire (que l’on peut représenter par une matrice unitaire). Le caractère linéaire de notre fonction vient du fait que l’équation d’onde qui nous occupe est linéaire ; de son côté, l’unitarité correspond à la conservation de l’énergie. |









