Et si la mousse à raser était la solution à l’un des problèmes majeurs du XXIème siècle ?

Le problème dont je parle, c’est celui de la pollution sonore. La gêne liée au bruit est en effet bien loin d’être anecdotique. Selon un rapport de l’Organisme Mondial de la Santé ¹, la pollution atmosphérique est la plus importante en matière d’impact néfaste sur la santé humaine… mais juste après, en deuxième position de ce palmarès peu réjouissant se trouve la pollution sonore. Toujours selon l’OMS, cette dernière est une véritable menace pour la santé publique : les « désagréments » qu’elle engendre vont des acouphènes aux troubles de l’apprentissage en passant par les perturbations du sommeil… mais également les crises cardiaques. On ne devrait pas parler de confort acoustique mais plutôt de survie acoustique !

Le problème étant posé, que vient faire la mousse à raser là-dedans ? Elle est en fait un exemple d’une famille de mousses plus générale : les mousses liquides. Comme la mousse du capuccino ou celle utilisée dans certains extincteurs. Ce type de matériau se compose de deux phases, l’une gazeuse (le plus souvent de l’air) et l’autre liquide, qui en constitue le squelette. De fines membranes liquides, les films de savon, séparent les bulles les unes des autres et satisfont les lois de Plateau : les films se rejoignent par trois pour former des canaux liquides (également appelés Bords de Plateau) qui contiennent la majorité du liquide de la mousse².

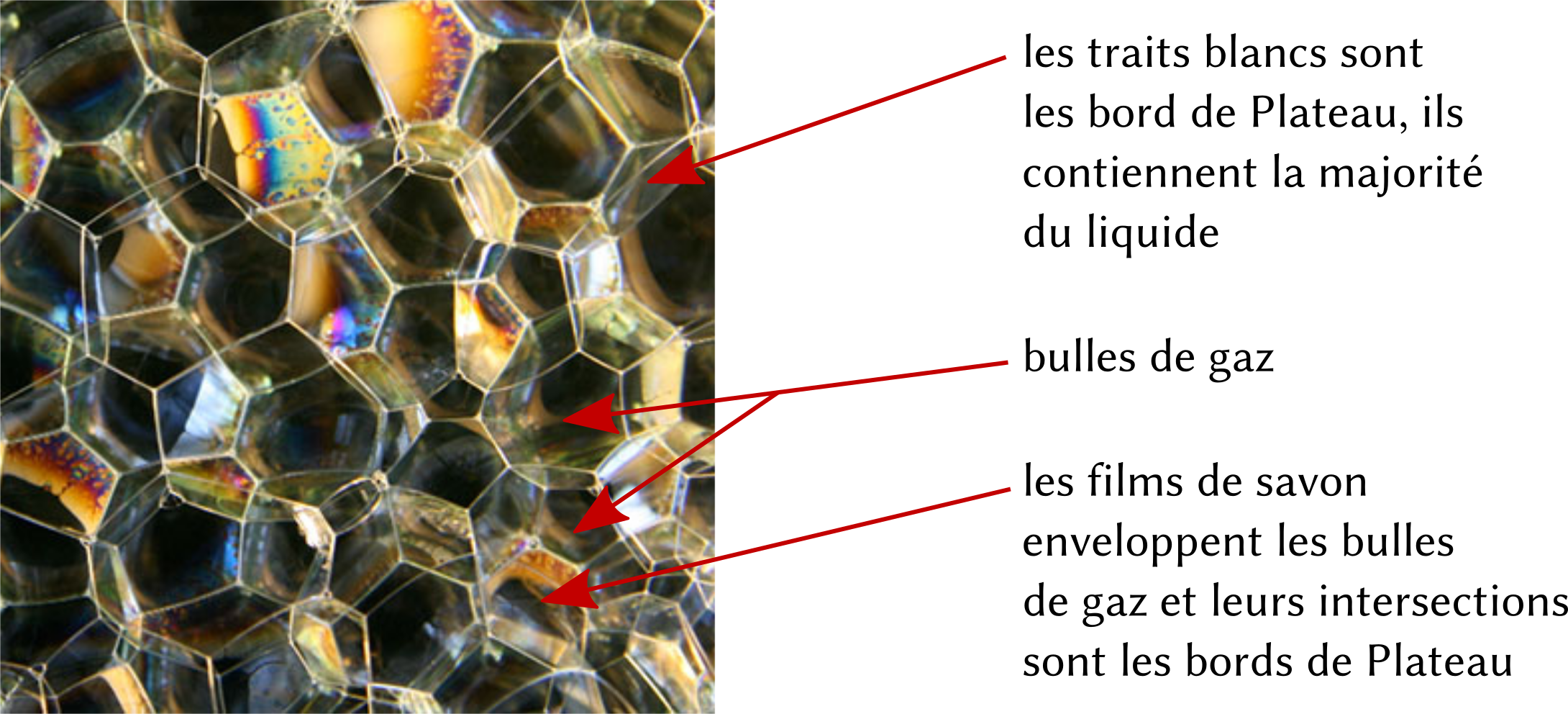
Ces deux éléments clés de la mousse, membranes et canaux liquides, sont évidemment déformables et mobiles. Une des manières de les mettre en mouvement est d’émettre du son, la vibration se propageant alors à l’intérieur de la mousse.

Maintenant, les ingrédients sont réunis : le son et la mousse. Ce qui m’intéresse tout particulièrement durant ma thèse, c’est d’étudier la manière dont le son est dissipé par les mousses. Mon équipe a réalisé il y a quelques années des mesures ultrasonores, sur les mousses liquides³. La réponse du matériau face à cette sollicitation montre différents régimes, en fonction de la fréquence. Une modélisation fondée sur une vision très simple et schématique de la mousse liquide a permis de les expliquer.

À basse fréquence (dans le domaine ultrasonore, donc tout de même à quelques centaines de kHz), canaux liquides et membranes se déplacent ensemble, tandis qu’à haute fréquence, les canaux demeurent immobiles en raison de leur inertie et seuls les films se déplacent. Entre les deux, on observe un régime dans lequel les canaux liquides se déplacent faiblement, alors que les membranes ont un mouvement de bien plus grande amplitude, effectué en opposition de phase. Ce dernier régime correspond à la résonance, associée à un maximum de l’atténuation du son par la mousse. Les membranes y jouent donc un rôle majeur.

Cependant, l’emploi de mousses liquides pour lutter contre les nuisances sonores semble peu réaliste, étant donné leur manque de stabilité dans le temps. Avec la gravité, le liquide contenu dans la mousse s’écoule, et avec le temps il ne reste plus de la mousse qu’une faible étendue liquide. Des mousses solides, qui savent donc mieux se tenir, existent et sont déjà employées comme matériau d’isolation acoustique. Toutefois, ces mousses-là ne comportent généralement pas de membrane.
Puisque le rôle joué par les membranes dans les mousses liquides a été démontré, notre idée est de s’en inspirer pour explorer une nouvelle classe de matériaux : des mousses solides avec des membranes. Ces matériaux inédits existent déjà, en réalité. Lors du procédé de fabrication d’une mousse solide, celle-ci passe d’abord par une phase liquide, ayant donc des membranes, avant que l’ensemble ne se solidifie. Les fabricants considèrent les membranes inutiles pour leurs applications (principalement du rembourrage de sièges automobiles), aussi les détruisent-ils généralement à l’aide d’un puissant écoulement d’air chaud dans la mousse.  Grâce à un partenaire industriel, nous pouvons obtenir des échantillons de mousses parfaitement identiques (de même composition chimique, avec une structure interne –porosité, taille des pores – identique), certains sans membranes et d’autres pour lesquels elles ont été préservées. Les conditions expérimentales sont idéales pour tester l’influence de ces membranes sur les performances acoustiques.

Les expériences sont réalisées à l’aide d’un dispositif expérimental très répandu en acoustique : le tube d’impédance, aussi appelé tube de Kundt. A l’une des extrémités d’un tube est situé un haut-parleur, tandis qu’à la seconde est placé l’échantillon de mousse. Le son se propage d’abord dans l’air à l’intérieur du tube, avant de pénétrer dans le matériau, puis d’être réfléchi au fond du tube. Trois microphones permettent de mesurer les changements de pression dus à la perturbation de l’onde acoustique, deux placés en amont du matériau pour mesurer le son réfléchi, et le troisième placé après l’échantillon de sorte à mesurer le son transmis. Il est ainsi possible de mesurer les performances acoustiques de la mousse en réflexion, via le coefficient d’absorption, et en transmission afin de déterminer l’efficacité pour l’isolation phonique.

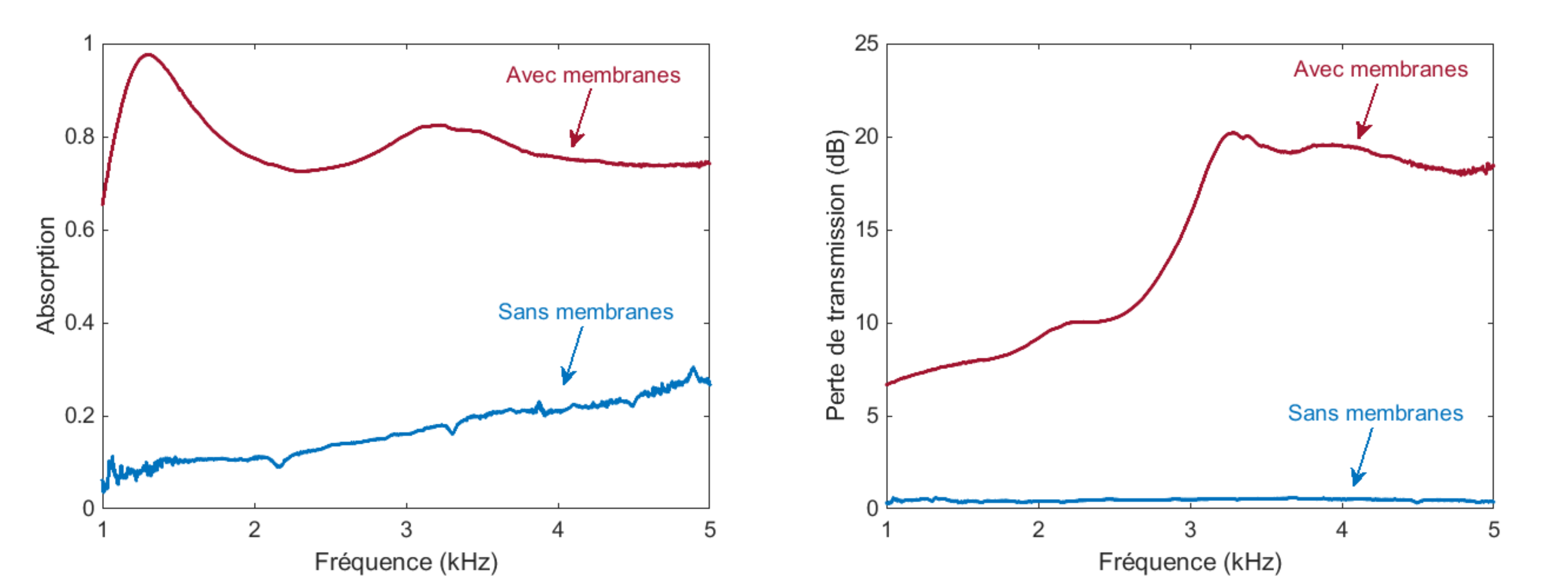
Les résultats en absorption et en perte de transmission sont sans ambiguïté : la présence des membranes augmente considérablement les performances acoustiques ! ⁴

Une bonne absorption permet ainsi d’avoir une ambiance agréable au sein de la pièce elle-même (par exemple pour discuter sans être gêné par une forte réverbération, comme c’est le cas dans les gymnases ou piscines). La perte de transmission traduit quant à elle la qualité de l’isolation face aux bruits environnants (voisinage et extérieurs).

La transmission acoustique a également été enregistrée en plaçant les deux échantillons de mousse l’un après l’autre au-dessus d’un haut-parleur. Pendant les 5 premières secondes de l’enregistrement audio, aucun échantillon ne couvre le haut-parleur. Pendant les 5 suivantes, l’échantillon de mousse sans membranes est placé devant : aucune différence n’est entendue, ce qui correspond bien à la courbe de perte par transmission, quasiment nulle sur toute la gamme de fréquence. Enfin, pendant les 5 dernières secondes, c’est l’échantillon avec membranes qui est placé devant le haut-parleur : on peut entendre une baisse du volume sonore, et constater que les basses fréquences sont davantage transmises que les aigus, que l’on n’entend presque plus (ce qui est à nouveau cohérent avec la courbe de perte par transmission, présentant des valeurs plus importantes d’atténuation pour les hautes fréquences).

Grâce à leur finesse – seulement quelques microns – ainsi que leur déformabilité, les membranes sont mises en vibration par l’onde acoustique, et transmettent donc l’onde à l’intérieur du matériau où la dissipation se produit sous forme de pertes visqueuses et thermiques. Par ailleurs, la vibration des membranes pourrait également être transmise au reste de la partie solide de la mousse, entraînant une vibration structurelle plus importante que dans le cas des mousses sans membranes (pour lesquelles on considère généralement que la phase solide demeure immobile).

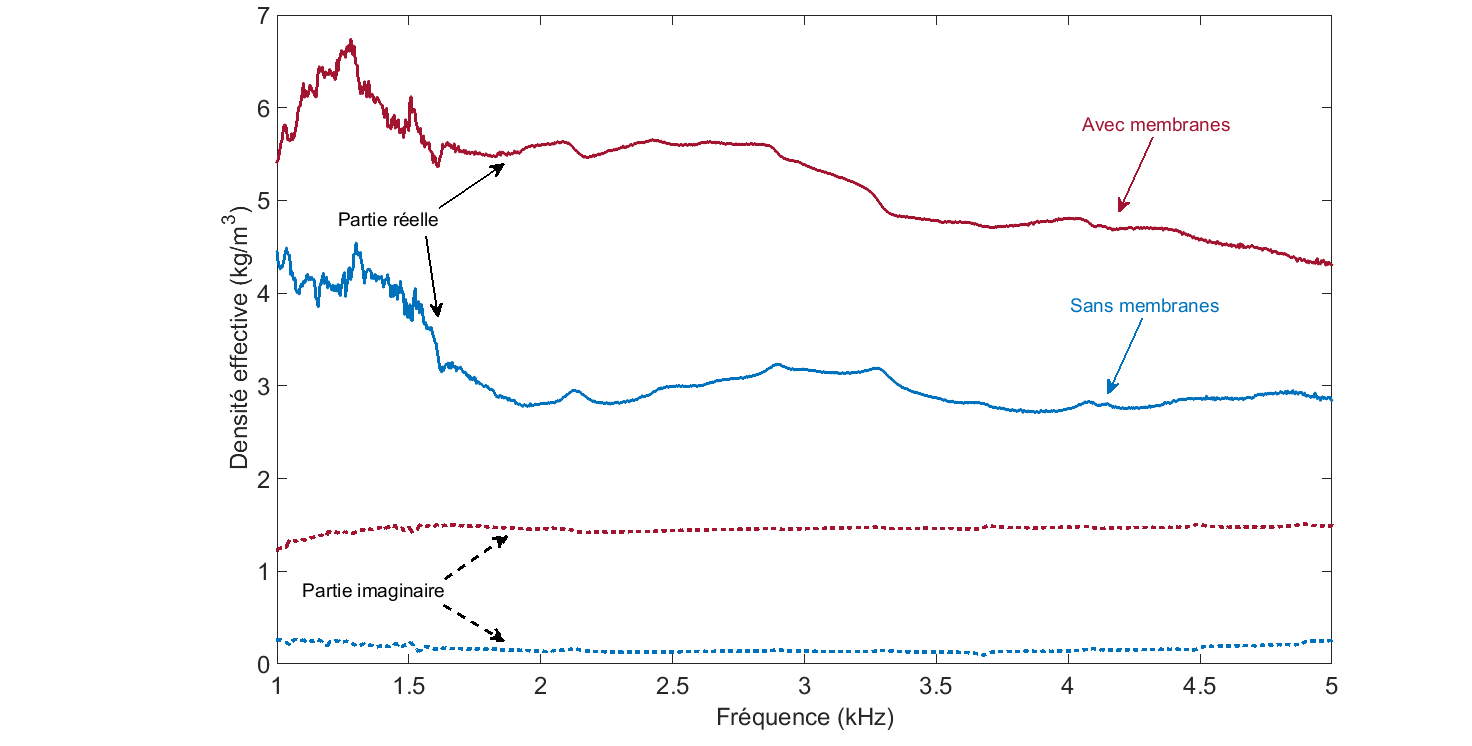
Enfin, en plus de l’absorption et de la transmission acoustique, nos mesures nous permettent de déduire davantage d’informations sur la mousse et ses propriétés effectives. La mousse peut en effet être vue comme un milieu effectif homogène, et non plus comme un matériau hétérogène composé de deux phases, liquide et gazeuse. Ce milieu effectif a des propriétés qui sont généralement différentes de la simple moyenne des propriétés des deux phases, dans leurs proportions respectives. La mousse est ainsi caractérisée par sa densité et sa compressibilité effectives, qui sont deux grandeurs complexes (intervenant entre autre dans le calcul de la vitesse du son). Leur partie réelle est à comparer à la « véritable » valeur physique, par exemple celle que l’on obtiendrait en pesant l’échantillon pour la densité. Leur partie imaginaire contient quant à elle l’information sur la capacité à dissiper le son.^a 

On constate que la densité est grandement affectée par la présence des membranes, alors que l’ajout de masse est négligeable. En d’autres termes, peser les deux échantillons de mousse avec et sans membranes donne le même résultat, mais les propriétés effectives sont quant à elles très différentes. L’augmentation de la partie imaginaire de cette densité, avec les membranes, est directement liée à l’augmentation de la dissipation qui se traduit donc également sur l’absorption et la transmission.

Il nous reste désormais à identifier les mécanismes physiques à l’origine de ces changements de densité effective, pour mieux comprendre la dissipation et ainsi, à l’avenir, optimiser les mousses et réduire encore plus efficacement les nuisances sonores ! Et tout ceci grâce à la mousse à raser qui, même si elle restera sur le menton et non dans les cloisons, aura été source d’inspiration.