Comment les réservoirs magmatiques se remplissent-ils ?

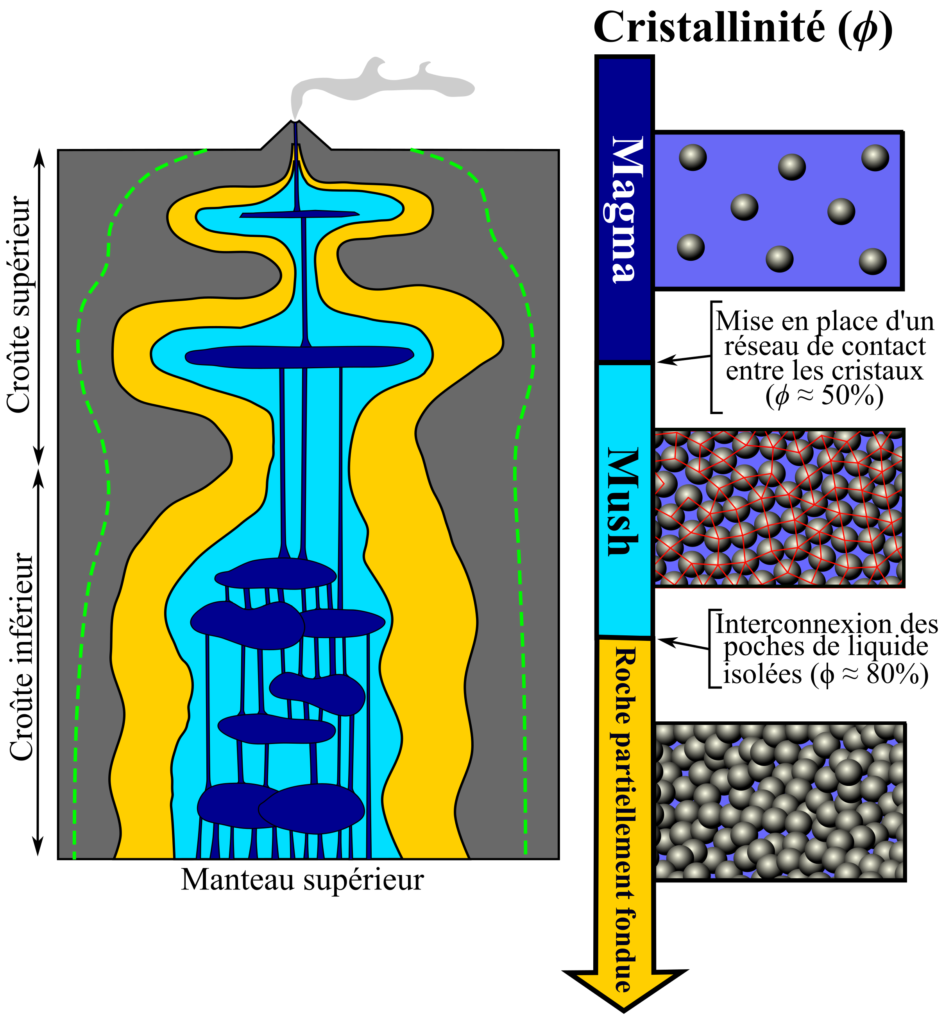
Les éruptions volcaniques sont le résultat visible en surface de processus chimiques et physiques qui se produisent dans les réservoirs magmatiques. Il y a encore quelques décennies, on imaginait que ces réservoirs magmatiques étaient composés d’une grande poche remplie de roches fondues appelée la chambre magmatique. Aujourd’hui, on pense plutôt que les chambres magmatiques ne sont présentes que de façon éphémère : le magma présent dans la chambre va refroidir et progressivement précipiter des cristaux, en raison du contact avec la croûte terrestre plus froide. A partir d’une certaine proportion de cristaux (cristallinité), les cristaux commencent à se toucher et former un squelette semi-rigide qui inhibe grandement la capacité du magma à s’écouler. On parle alors de mush magmatique. Pour des cristallinités encore plus importantes, la phase liquide n’est présente plus que sous la forme de petites poches isolées et on parle alors de roches partiellement fondues.

Le mush magmatique et les roches partiellement fondues (Fig. 1) ne peuvent pas facilement s’écouler et être émis lors d’une éruption à cause du squelette semi-rigide formé par les contacts entre les cristaux. C’est notamment le cas pour les volcans endormis depuis des centaines ou milliers d’années dont les réservoirs magmatiques sont probablement uniquement composés de mush et de roches partiellement fondues. Cependant, il y a de nombreux exemples où des volcans endormis se réveillent soudainement. Prenez par exemple le Mont Komagatake situé sur l’île de Hokkaido au Japon qui s’est réveillé violemment en l’an 1640 après ~5000 ans sans activité, ou encore plus récemment l’éruption du Mont Pinatubo le 2 Avril 1991 après environ 500 ans de repos (Fig. 0). Dans ces scénarios éruptifs, on remarque souvent dans la composition des laves émises qu’une intrusion de magma, plus chaud et moins cristallin, s’est mise en place dans le réservoir quelques temps avant l’éruption. La mise en place d’une intrusion dans un réservoir apporte matière et chaleur au réservoir afin de le réactiver, c’est-à-dire générer un volume de magma éruptible (une chambre magmatique) à partir d’un mush en déstabilisant les chaînes de contacts existantes entre les cristaux.

Pour tenter de comprendre quels sont les mécanismes physiques contrôlant cet important processus, les volcanologues ont proposé différentes hypothèses pour expliquer la génération de magma éruptible suite à la mise en place d’une intrusion dans un mush magmatique. On peut les répartir en deux grandes catégories en fonction du régime de mise en place de l’intrusion. Dans la première catégorie, l’intrusion se met en place à la base du mush et vient le réchauffer comme le ferait une plaque de cuisson avec une casserole. La diffusion de la chaleur de l’intrusion permet de faire fondre des cristaux du mush, ce qui va déstabiliser le réseau de contact et générer du magma mobile et éruptible. Dans cette famille de scénarios, l’interaction entre le mush résident et l’intrusion est limitée à des transferts de chaleur et parfois de gaz exsolvé. Dans le second type de scénarios, l’écoulement du magma intrusif permet d’entraîner les cristaux et de déstabiliser les chaînes de contacts afin de créer une zone fluidisée. Le magma intrusif s’écoule ensuite lentement à travers le mush dans ce chemin fluidisé (illustré par les flèches blanches dans la figure 4b). Au contraire du premier type de scénario, la fluidisation du mush par l’intrusion est marquée par une interaction importante entre ces deux matériaux et un mélange efficace. Le régime de mise en place d’une intrusion va donc exercer un important contrôle sur les mécanismes de réactivation et d’ évolution du réservoir magmatique. Il est donc important de comprendre quelles sont les propriétés physiques qui contrôlent la mise en place d’une intrusion dans un réservoir  afin de pouvoir savoir laquelle de ces hypothèses est la plus plausible.

Pour estimer comment une intrusion se met en place dans un réservoir magmatique, les volcanologues ont souvent utilisé le contraste entre les densités d’ensemble de l’intrusion et du mush. L’hypothèse classiquement faite est que l’intrusion se met en place à la base du mush lorsque la densité d’ensemble de l’intrusion est la plus importante. Au contraire, lorsque la densité d’ensemble de l’intrusion est inférieure à celle du mush, on s’attend plutôt à la fluidisation des cristaux présents dans le réservoir. Le problème avec cette hypothèse est qu’elle n’avait jamais été réellement validée. Les expériences réalisées en laboratoire^​1,2​  reproduisant le remplissage d’un réservoir magmatique ont été effectuées en utilisant uniquement des liquides et négligent la nature multiphasée des matériaux magmatiques. Lors de ces expériences, la densité des liquides utilisés comme matériaux résident et intrusif était choisie afin de reproduire les contrastes entre les densités d’ensemble de l’intrusion et de son matériel résident. De ce fait, la validité de l’hypothèse que les écoulements magmatiques sont contrôlés par les contrastes de densité d’ensemble était communément acceptée par les volcanologues mais n’avait jamais été réellement validée.

Afin de tester cette hypothèse, au cours de ma thèse au sein de l’équipe géophysique des volcans du laboratoire ISTerre, j’ai simulé numériquement la mise en place d’une intrusion de magma dans un réservoir riche en cristaux. Pour cela, nous simulons à l’aide de programmes informatiques la dynamique de l’écoulement couplé de la phase liquide et des cristaux. Pour le liquide, nous résolvons les fameuses équations de Navier-Stokes sur un maillage régulier et fixe (Fig. 2). Pour la phase solide, chaque cristal est représenté par une sphère dont le mouvement est simulé en calculant les forces externes qui lui sont appliquées et en résolvant la seconde loi de Newton. Pour les forces, nous prenons en compte la gravité, la pression statique (a.k.a. la poussée d’Archimède), la pression dynamique (liée à l’écoulement de la phase liquide), les frottements visqueux avec liquide, et les contacts frictionnels entre les cristaux. Les simulations sont calculées en progressant par petits pas de temps (10^-5 secondes ici) au cours desquels la dynamique du liquide est mise à jour et les forces externes appliquées aux cristaux sont recalculées.

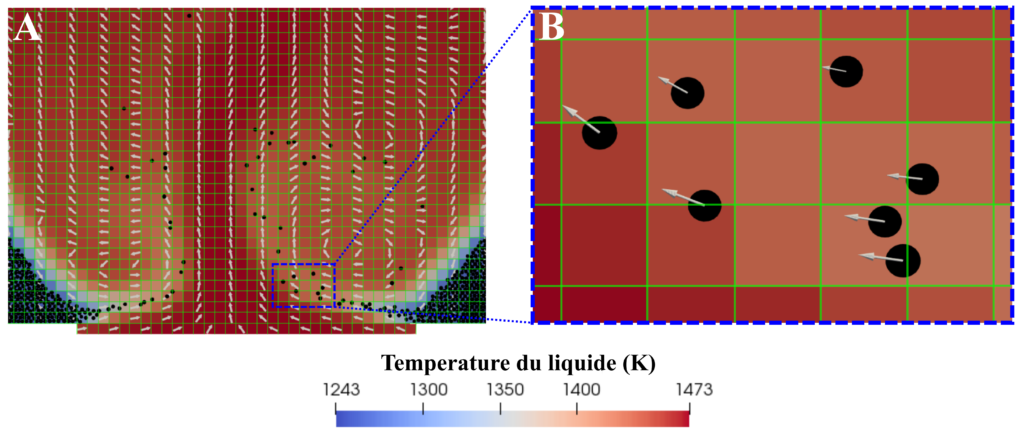
Dans la théorie, c’est très simple comme simulation, mais dans la pratique, c’est beaucoup plus complexe. Imaginez que l’on veuille simuler 100 secondes d’une simulation comprenant 10⁵ cristaux. Cela implique de calculer les forces externes appliquées aux particules 10¹² fois. Chaque estimation des forces externes demande ensuite des étapes intermédiaires qui sont simples mais nombreuses. Du coup, ça fait beaucoup de calculs et cela nous oblige à paralléliser le code, c’est à dire effectuer le calcul sur de nombreux cœurs de processeurs (128 pour chaque simulation). Les simulations ont été effectuées sur les clusters de calcul du mésocentre CIMENT ^​*​ de l’université Grenobles-Alpes pendant plusieurs semaines, voire mois, selon la durée de la simulation.

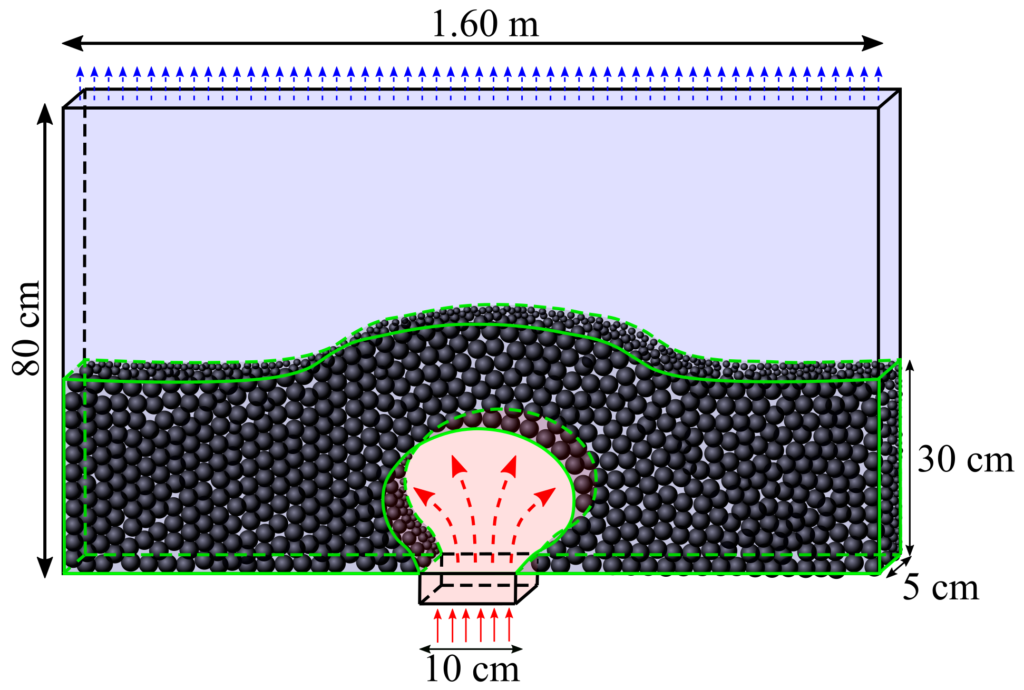
Pour faire nos expériences numériques, nous avons défini un réservoir rempli avec un liquide visqueux. Afin de répliquer les conditions d’un mush magmatique, nous avons simulé la sédimentation de cristaux (ici des sphères) afin de former un lit de particules d’une épaisseur de 30 cm à la base du réservoir (Fig 3). Pour simuler la mise en place d’une intrusion de magma dans le réservoir, nous avons injecté à une vitesse constante un liquide ayant une densité et une viscosité différentes du liquide présent initialement dans le réservoir. Afin de déterminer quels sont les paramètres physiques contrôlant le régime de mise en place d’une intrusion, nous avons effectué plusieurs simulations en faisant varier les contrastes de densité et de viscosité entre les deux matériaux et la vitesse d’injection. Pour analyser nos simulations, nous les avons comparés entre elles en fonction des contrastes entre les densités des phases liquides (qui ne prend pas en compte la présence des cristaux) de l’intrusion et du mush hôte, \( \rho_\mathrm{i} – \rho_\mathrm{h}\) , des  contrastes de densité d’ensemble (qui prend en compte les cristaux) \( \rho_\mathrm{i}^\star – \rho_\mathrm{h}^\star \) , et des contrastes entre les viscosités dynamiques des phases liquides, \( \eta_\mathrm{h} / \eta_\mathrm{i} \).

Grâce à ces simulations, nous avons identifié trois régimes d’intrusions :

• Ascension : une instabilité de Rayleigh-Taylor se produit permettant à un volume de l’intrusion de rapidement s’écouler à travers et au dessus du lit de particules en entraînant des cristaux du mush (Fig. 3 et 4A).
• Fluidisation : ce régime est caractérisé par un écoulement lent et vertical du liquide injecté dans le lit de particules, permettant de déstabiliser les contacts entre les particules et faisant diminuer la cristallinité (Fig. 4B).
• Écoulement latéral : le liquide injecté s’écoule horizontalement le long de la base du réservoir (Fig. 4C). Cet écoulement latéral permet l’entraînement des cristaux présents dans le réservoir et génère deux tourbillons contre-rotatifs de chaque côté de la zone d’injection.

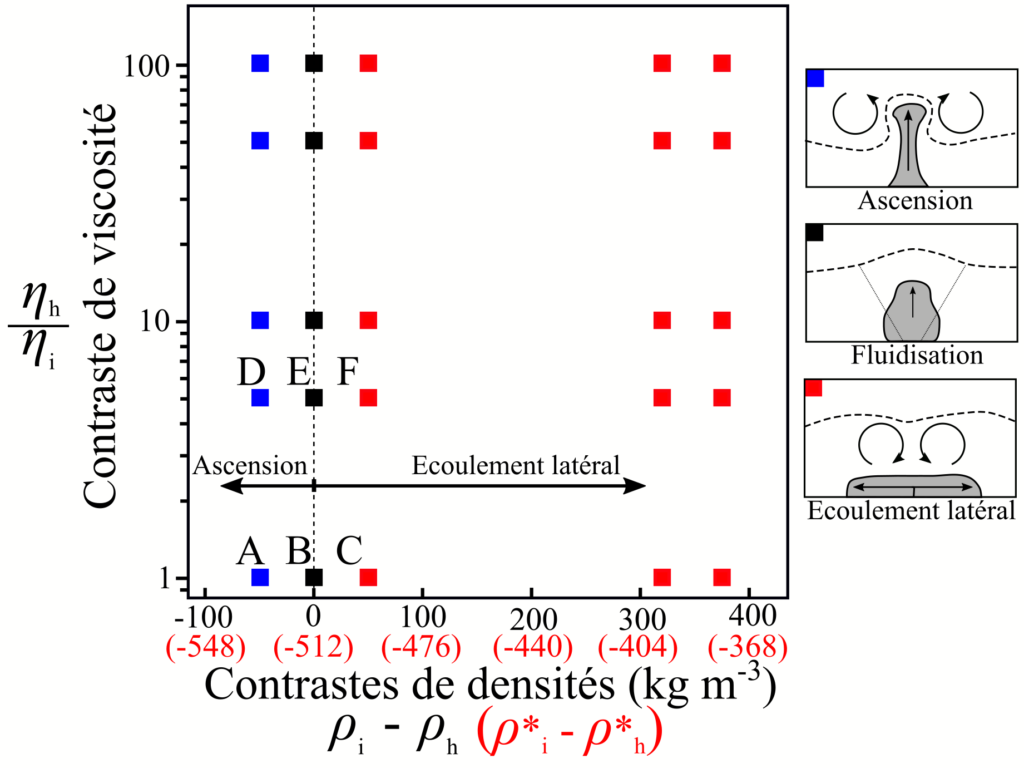
Nous avons effectué une série de 25 simulations en utilisant différents contrastes de densité et de viscosité entre les phases liquides du mush et du magma injecté et en conservant un même flux d’injection afin de réaliser un diagramme des régimes (Fig. 5). Sur ce diagramme, les trois couleurs représentant les trois régimes d’intrusion présentent un bon tri horizontalement le long de l’axe correspondant aux deux contrastes de densité. Au contraire, on n’observe pas de tri des simulations verticalement, c’est-à-dire en fonction du contraste de viscosité entre l’intrusion et le mush. Cela montre bien que les contrastes de viscosité n’ont pas une grande importance sur la géométrie d’une intrusion, qui est principalement contrôlée par les contrastes de densité. Si l’on s’intéresse de plus prêt à la distribution des régimes le long de l’axe des abscisses, on remarque que c’est le contraste entre les densités des phases liquides du magma intrusif et du mush qui contrôle l’emplacement de l’intrusion et non la différence entre leurs densités d’ensemble. En effet, lorsque \( \rho_\mathrm{i} – \rho_\mathrm{h} < 0 \), on observe un régime d’ascension, alors que dans les cas où \( \rho_\mathrm{i} – \rho_\mathrm{h} > 0 \), l’intrusion se met en place en écoulement latéral. Enfin lorsque,  \( \rho_\mathrm{i} – \rho_\mathrm{h} = 0 \), l’intrusion se met en place en fluidisant le mush. Si l’hypothèse du contrôle par les contrastes de densité d’ensemble était juste, toutes les simulations que nous avons effectuées auraient dû se trouver dans le régime d’ascension car elles présentaient toutes un mush ayant une densité d’ensemble supérieure à celle de l’intrusion \( \rho_\mathrm{i}^\star – \rho_\mathrm{h}^\star < 0 \).

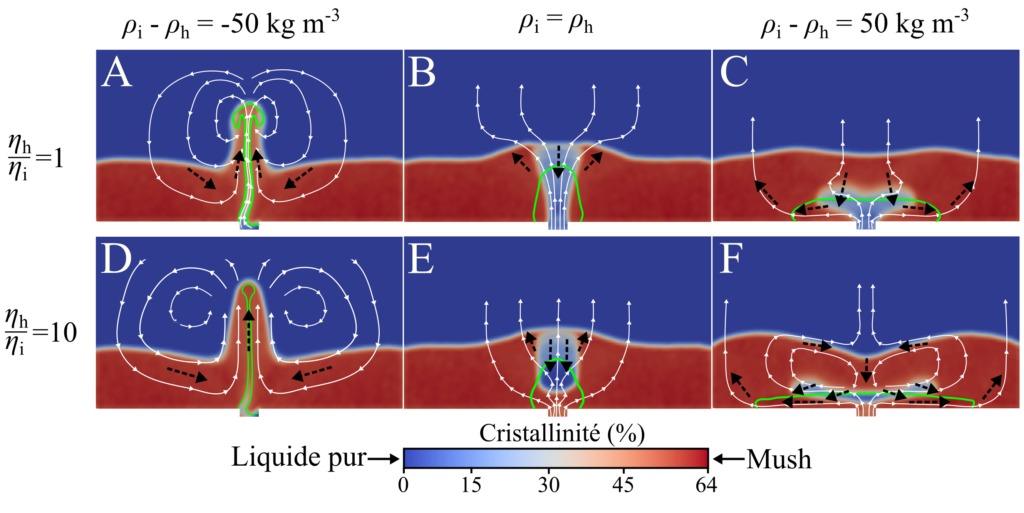
Lorsque que l’on regarde en détail l’influence du contraste de viscosité, \( \eta_\mathrm{h} / \eta_\mathrm{i} \) , on remarque que cela affecte la dynamique des écoulements dans le mush lors la mise en place de l’intrusion mais ne change pas le régime d’intrusion. Pour le régime de fluidisation, augmenter le contraste de viscosité accentue la diminution de la cristallinité dans la zone fluidisée située au sommet de l’intrusion (Fig. 4D). Pour le régime d’écoulement latéral, on observe une diminution de l’épaisseur de l’intrusion et une augmentation de l’entraînement d’écoulement dans le mush (Fig. 4E). Enfin, l’augmentation du contraste de viscosité dans le régime d’ascension génère un entraînement plus important du mush par la remontée rapide de l’intrusion (Fig. 4F).

Nos simulations numériques nous ont donc permis de montrer que ce sont les contrastes de densité entre les phases liquides de magma intrusif et du mush hôte qui sont le plus important pour la géométrie d’une intrusion. Le contraste de viscosité exerce quant à lui un contrôle de second ordre sur la dynamique de mise en place de l’intrusion. Ces résultats permettent d’invalider l’hypothèse que les écoulements dans les réservoirs magmatiques seraient contrôlés par les contrastes de densité d’ensemble. Cette hypothèse était à la base de nombreuses idées en volcanologie et nos résultats devraient permettre de reconsidérer notre compréhension des réservoirs magmatiques et de leurs dynamismes. 

Dans notre étude, nous nous sommes également intéressés à l’influence que peut avoir la vitesse d’injection sur la géométrie d’une intrusion et comment nos résultats se mettent en perspective avec les observations qui peuvent être faites par les volcanologues sur le terrain. Si vous souhaitez en apprendre plus sur nos résultats et simulations, je vous invite à découvrir notre article^​3​.