Dans une vidéo de vulgarisation récente, une étudiante rencontre des physiciens et compile leurs réactions face à une tasse de café. Le résultat est remarquable, comme la diversité des réponses proposées. En ce qui me concerne, mon traditionnel café du matin me laisse toujours perplexe : comment se fait-il que l’on sache prédire l’occurrence des éclipses pour les siècles à venira ou encore mesurer des constantes fondamentales avec une incertitude relative de moins d’un pour cent millions, mais que l’on soit incapable de savoir si ma tasse va déborder suite à tel ou tel mouvement ? Nous allons aborder ensemble ce problème, appelé ballottement, et découvrir ce qui est actuellement connu ainsi que ce qu’il reste à élucider.
Résonance d’un verre d’eau
Pour cela, munissez-vous d’un récipient rempli d’eau à mi-hauteur, comme un verre, une tasse, ou encore une bouteille, et déposez-le près de vous (mais loin de votre ordinateur !). Si la surface de votre café se déforme lorsque vous marchez, c’est qu’à chaque pas la tasse est légèrement accélérée puis ralentie. Répétons ce phénomène : bougez votre récipient d’avant en arrière d’abord lentement, disons un aller-retour en deux secondes, puis augmentez progressivement la fréquence du mouvement. Vous allez remarquer que le liquide n’est pas sensible à toutes les vibrations et que sa surface reste l’essentiel du temps peu déformée. En revanche, certaines fréquences d’oscillation ont un effet notable sur la surface, qui se met par exemple à ressembler à l’une de celles dessinées sur la figure 1 : on parle de résonance à cette fréquence propre.

On sait depuis près de 200 ans prédire ces fréquences propres, grâce aux travaux du physicien français Siméon Denis Poisson, dont le travail à ce sujet est aujourd’hui disponible librement sur internet.b Dans notre cas, on modélise la tasse par un cylindre de rayon \(R\) suffisamment rempli, c’est-à-dire tel que la hauteur de liquide soit supérieure à \(R\). On sait alors simplement calculer la fréquence propre la plus petite \(f_0\),
\[f_0=\frac{1}{2\pi}\sqrt{\frac{1,8412~g}{R}}.~~~~~~~~~~~~~~~~~ (1)\]
Dans cette équation, \(f_0\) s’exprime en hertz, \(g=9,81~\mathrm{m}\cdot\mathrm{s}^{-2}\) est l’accélération de la pesanteur, \(1,8412\) est une constante numérique issue du calcul et \(R\) est le rayon de la tasse (en mètres) : pour une valeur typique de \(R=3~\mathrm{cm}\), on obtient \(f_0\simeq 4~\mathrm{Hz}\), c’est-à-dire quatre aller-retours par seconde. Si l’on passe à un réservoir plus grand, par exemple une casserole, cette fréquence diminue rapidement (pour \(R=10~\mathrm{cm}\), on évalue \(f_0\simeq 2~\mathrm{Hz}\)) ; cette tendance est facilement observable chez vous, vérifiez-là !
De nombreuses équipes scientifiques ont comparé les prédictions de Poisson à leurs résultats expérimentaux, et les deux coïncident remarquablement. Si l’on souhaite éviter le débordement d’un récipient ou encore la formation de gouttes, la solution est donc simple : il suffit d’éliminer les vibrations qui correspondent à ces fréquences propres.
Oscillations forcées à résonance
En pratique, si l’on sait diminuer l’amplitude de certaines vibrations, on ne peut jamais les annuler totalement. L’enjeu consiste alors à déterminer la vibration maximale admissible, par exemple celle menant le liquide à la limite de débordement, pour être certain de ne pas la dépasser. Pour cela, supposons que l’on fasse bouger horizontalement le réservoir à la fréquence propre \(f_0\) et cherchons l’amplitude de la perturbation engendrée. On la note \(A\) et on la définit comme la hauteur à laquelle le liquide monte sur le bord du réservoir en un point donné (situé selon la direction d’oscillation). En considérant toujours un récipient cylindrique et suffisamment rempli, on peut montrer à partir des équations de la mécanique des fluides que la grandeur \(A\) vérifie l’équation suivante
\[\underbrace{\frac{\mathrm d^2A}{\mathrm dt^2}}_{(1)}+\underbrace{\frac{2\pi f_0}{Q}\frac{\mathrm dA}{\mathrm dt}}_{(2)}+\underbrace{(2\pi f_0)^2A}_{(3)}=\underbrace{F\cos(2\pi f_0t)}_{(4)}~~~~~~~~~~~~(2)\]
Résoudre cette équation permet de prédire l’évolution de l’amplitude \(A(t)\). Chaque terme correspond à un effet bien particulier :
- décrit l’inertie du fluide, c’est-à-dire sa tendance à conserver son mouvement.
- rend compte de la dissipation et fait intervenir le nombre \(Q\) appelé facteur de qualité. En l’absence de force, la surface d’un fluide dans un récipient initialement perturbé redeviendra plane en effectuant typiquement \(Q\) oscillations : cela est cohérent avec le fait que lorsque \(Q\) est grand, l’amortissement devient faible et ce terme (2) petit. Tout comme \(f_0\), on dispose d’une formule permettant de calculer \(Q\).c
- traduit l’effet de la gravité. Si le liquide est monté sur la paroi, cette force le pousse vers le bas, et inversement s’il est situé en-dessous du niveau moyen : on parle d’une force de rappel.
- est relié à la vibration appliquée : on retrouve sa fréquence et on sait calculer la grandeur à partir de l’amplitude d’oscillation du récipient.
L’équation (2) est souvent rencontrée en physique pour décrire des phénomènes oscillants, comme ceux observés dans un diapason ou dans un cristal de quartz. On sait de plus la résoudre exactement, la solution étant
\[A(t)=\frac{FQ}{(2\pi f_0)^2}\sin(2\pi f_0t)~~~~~~~~~~~~~~~~~ (3)\]
Connaissant les valeurs numériques de \(F\), \(Q\) et \(f_0\), on peut calculer la hauteur maximale à laquelle montera le liquide. Le problème semble donc résolu, et on a à disposition une expression permettant de prédire ce qu’il se passe dans verre d’eau ou tout autre récipient que l’on déplace.
Le rôle du ménisque
Ces prédictions théoriques ont été confrontées de nombreuses fois aux résultats d’expériences. Pour cela, il faut se placer dans des conditions plus contrôlées qu’un simple verre bougé à la main. En pratique, on utilise souvent un autre liquide que l’eau, dont la surface se pollue rapidement lorsque laissée à l’air libre, ainsi que des instruments précis pour réaliser la vibration et mesurer la déformation engendrée.
Par exemple, une photographie du dispositif que nous avons utilisé est reportée figure 2: un vibreur (à droite, hors champ) fait osciller l’ensemble du dispositif, surélevé pour empêcher les frottements avec la table. Le fluide dans le cylindre central n’est pas de l’eau mais de l’hexafluorure de soufre (SF\(_6\)), et est présent à moitié sous forme liquide, à moitié sous forme de gaz. Sa température est contrôlée à l’aide d’une circulation d’eau, dont les tuyaux sont visibles des deux côtés, et son mouvement est enregistré en suivant le déplacement d’un faisceau laser dévié au niveau de l’interface (le laser est visible au dessus de la cellule).

On commence par calculer la fréquence propre \(f_0\), et on fait osciller ce dispositif à cette fréquence : la surface se met nettement en mouvement et on observe bien une résonance. Pour l’instant tout se passe comme prévu, et cela confirme que l’on dispose de méthodes fiables pour déterminer les fréquences contre lesquelles un réservoir doit être protégé pour limiter les éclaboussures ou débordements.
Passons ensuite à une vérification de l’équation (3). Pour cela, on mesure d’une part \(A(t)\), et on calcule d’autre part le membre de droite à partir des paramètres de l’expérience. Résultat : bien que \(A(t)\) soit expérimentalement sinusoïdal et proportionnel à \(F\), ça ne colle pas, et tout se passe comme si la formule donnant accès à \(Q\) était fausse. Nous ne sommes pas les premiers à mettre cet effet en évidence, et cela fait maintenant presque trente ans que les résultats expérimentaux vont dans ce sens. Pour cerner l’origine du problème, il faut se rappeler que tout résultat en physique est associé à un certain domaine de validité. En reprenant les calculs ayant permis de démontrer les équations (2) et (3), on réalise qu’ils reposent sur une hypothèse majeure suivant laquelle les phénomènes qui se passent au niveau du ménisque sont supposés négligeables.
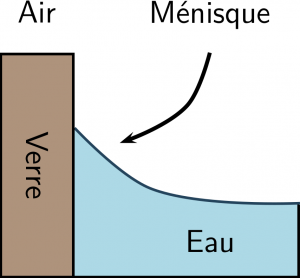
Le ménisque, c’est cette petite zone de quelques millimètres où un liquide se déforme légèrement pour s’accrocher à la paroi solide, comme schématisé à droite. Si vous regardez attentivement votre tasse de café ou votre verre d’eau, vous comprendrez immédiatement de quoi il est question.
On sait que prendre en compte l’existence d’un ménisque est indispensable pour comprendre les phénomènes qui affectent les objets de taille centimétrique, comme le mouvement d’une goutte sur une vitre. Ici, notre récipient a un rayon de quelques centimètres et le fait d’avoir négligé le ménisque est une hypothèse raisonnable pour expliquer le désaccord observé. Pour corriger l’écart entre prédiction théorique et expérience, la démarche semble donc simple. Il suffit de prendre en compte le ménisque dans les calculs afin d’obtenir une nouvelle expression pour le coefficient \(Q\), et donc pour l’équation (3), que l’on comparerait de nouveau avec les résultats expérimentaux. Le soucis, c’est qu’il s’agit d’un problème actuellement ouvert: personne ne sait prédire les mouvements de fluide ayant lieu dans un ménisque en mouvement oscillant, ni non plus les calculer numériquement !
L’apparition des non-linéarités
Continuons néanmoins à exploiter l’expérience, et supposons que l’on sache prédire la valeur corrigée de \(Q\), notée \(Q_\mathrm{cor}\). Le mouvement \(A(t)\) serait alors donné par l’équation (3) modifiée en conséquence,
\[A(t)=\frac{FQ_\mathrm{cor}}{(2\pi f_0)^2}\sin(2\pi f_0t).~~~~~~~~~~~~~~~~~ (4)\]
De manière générale, les équations (2) et (4) modélisent uniquement des systèmes proches de leur état d’équilibre, correspondant ici au cas où la surface du fluide est horizontale (\(A=0\)). Lorsque l’amplitude d’oscillation du fluide \(A\) devient suffisamment grande, disons supérieure à une amplitude critique \(A_\mathrm{c}\), on s’attend donc à ce qu’il apparaissent des effets dits non-linéaires qui modifient la dynamique du système et rendent tous les calculs bien plus délicats à mener.d
Notre expérience nous a permis de mesurer précisément et pour la première fois cette longueur \(A_\mathrm{c}\)1: il s’agit d’une grandeur appelée épaisseur des couches limites, caractérisant les mouvements de fluide proches des parois solides. Dans le cas de notre tasse de café, \(A_\mathrm{c}\) vaut une fraction de millimètre.
Ainsi, même si l’on parvenait à calculer la valeur corrigée du facteur de qualité \(Q_\mathrm{cor}\), par exemple en réussissant à mener un calcul prenant en compte l’effet du ménisque, les prédictions théoriques ne seraient valident que tant que la surface se déplace de moins d’un millimètre. Après cela, il faudrait en plus prendre en compte des effets non-linéaires.
Conclusion
La physique du ballottement, s’intéressant à l’évolution de liquides contenus dans des récipients en mouvement, reste pour moi fascinante par l’apparente trivialité du problème. Comme nous l’avons vu, si l’on sait précisément estimer les fréquences de vibrations auxquelles un récipient rempli est sensible, prédire l’évolution de ce système excité à résonance représente un réel défi théorique. Les difficultés proviennent de la prise en compte du ménisque, ainsi que des effets non-linéaires. Même si des solutions permettant d’éviter à un fluide agité de déborder existent déjà, consistant par exemple à fixer dans le liquide des plaques limitant les courants ou à disposer à sa surface des flotteurs rigides, il y a fort à croire que des avancées dans la compréhension de ces phénomènes mèneraient à des améliorations de ces dispositifs. Et juste par satisfaction personnelle, qui n’aimerait pas comprendre ce qu’il se trame dans une tasse de café ?
Notes
| a. | ↑ | Par exemple, l’éclipse solaire totale la plus longue du XXXe siècle débutera le 15 juillet 2903 à 23h55mn07.7s à côté de Balikpapan en Indonésie avant de se déplacer vers le milieu du pacifique sud où elle s’éteindra 7mn03.5s plus tard, comme expliqué sur le site de la NASA. |
| b. | ↑ | Comme de nombreux anciens articles scientifiques, sa lecture n’est pas aisée. En l’occurrence, des avancées en mathématiques, l’introduction des «fonctions de Bessel», font que l’on sait aujourd’hui établir les résultats de Poisson en quelques lignes. |
| c. | ↑ | En supposant que la surface du fluide est propre, c’est-à-dire que l’eau n’est pas recouverte de poussière ou autre impureté, on trouve \[Q=\frac{R}{1,8412}\sqrt{\frac{4\pi f_0}{\nu}}\] avec \(R\) le rayon du récipient (en mètres), donnée par l’équation (1) et exprimée en hertz, et \(\nu\) un paramètre du liquide appelé viscosité cinématique et valant dans le cas de l’eau \(\nu=1\cdot10^{-6}~\mathrm{m}^2\cdot\mathrm{s}^{-1}\). |
| d. | ↑ | L’exemple le plus connu de non-linéarité est celui du pendule simple de longueur \(\ell\) soumis à un champ de pesanteur \(g\), dont l’angle avec la verticale \(\theta\) vérifie en l’absence d’amortissement \[\frac{\mathrm d^2\theta}{\mathrm d t^2}+(2\pi f_0)^2\sin(\theta)=0,\hskip1cm f_0=\frac{1}{2\pi}\sqrt{\frac{g}{\ell}}\] Lorsque \(\theta\) est petit devant l’unité, \(\sin\theta\approx\theta\) et on retrouve l’équation (2) sans dissipation ni forçage ( (2) = (4) =0) . En revanche, si \(\theta\) est pris de plus en plus grand, il arrive un moment où l’approximation précédente n’est plus vérifiée, menant à des effets non-linéaires comme la perte d’isochronisme (la fréquence des oscillations n’est plus toujours \(f_0\) mais dépend de l’angle avec lequel le pendule est lâché). Dans cet exemple, on observe donc l’apparition d’effets non-linéaires lorsque \(\theta\) devient comparable ou supérieur à \(\theta_c=1~\mathrm{rad}\). |









