Après avoir lu le titre de cet article vous vous dites sûrement qu’utiliser des électrons pour voir n’a aucun sens, car tout le monde sait que la vision est associée à la lumière et vous avez bien raison. En effet, vous ne pouvez apprécier la beauté d’un tableau qu’à la seule condition que celui-ci soit éclairé … Mais si nous disposions d’un moyen de lui faire émettre de la lumière autrement qu’en l’éclairant, ne serions-nous pas capables de l’observer et de l’apprécier ? Après tout, c’est ce que vous faites tous les jours en allumant votre téléviseur. Vous utilisez de l’électricité pour émettre de la lumière à partir de l’écran, ce qui vous permet d’observer une image sur ce dernier. C’est avec cette idée en tête que je vous propose d’aborder cet article.
Voir des molécules ?
La diffraction limite le pouvoir de résolution des instruments d’optique. Typiquement, à partir du moment où la longueur d’onde de la lumière devient comparable à la taille de l’objet, ce dernier devient impossible à observer même avec le plus performant des microscopes optiques. C’est le cas pour une molécule dont la taille est plusieurs centaines de fois plus petite que la longueur d’onde de la lumière visible. En revanche, le spectre optiquea, obtenu en analysant la lumière émise par une molécule, contient beaucoup d’informations sur la molécule et son environnement. Ainsi, même s’il n’est pas possible d’observer optiquement les molécules comme le ferait un biologiste avec une bactérie sous son microscope, il est possible, grâce à la spectroscopie optique, d’obtenir une sorte de carte d’identité propre à la molécule étudiée. Mais alors, doit-on définitivement abandonner l’idée de réaliser des images de molécules ? En fait, nous allons voir dans la suite qu’il existe un appareil qui, à défaut de former des images optiques, permet de réaliser des sortes de topographies de molécules à une échelle de l’ordre du dixième de nanomètre. Mais avant cela, un peu d’explication sur le fonctionnement les spectroscopies optiques.
Le spectre optique : une carte d’identité de la molécule
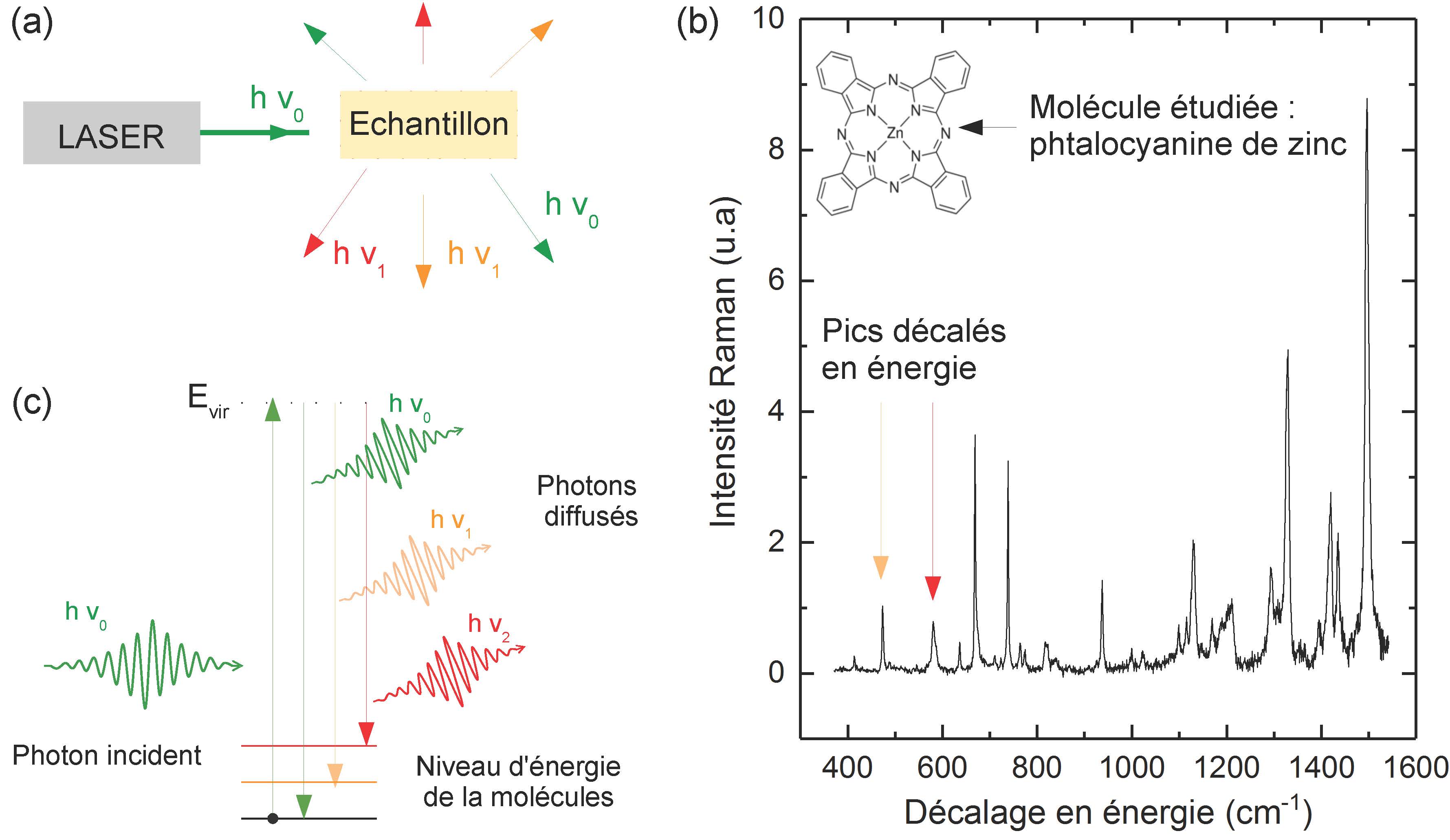
Lorsque l’on envoie de la lumière sur un échantillon, la lumière interagit avec les molécules de ce dernier en échangeant de l’énergie. Cet échange d’énergie va se traduire par un changement de longueur d’onde de la lumière émise par l’échantillon. Ainsi, en mesurant l’intensité de la lumière émise en fonction de la longueur d’onde, on peut construire le spectre optique caractéristique de la molécule. En particulier, pour identifier des molécules organiques les spectroscopies dites vibrationnelles, comme la spectroscopie Raman, sont très utilisées. Le principe de cette dernière est détaillé en Figure 1 : un échantillon composé d’une poudre de molécule donnéeb est éclairé par un laser à une fréquence \( \nu_0 \) (Fig.1 (a)), la lumière diffusée est ensuite analysée par un spectromètre, ce qui permet d’obtenir un spectre (Fig. 1 (b)). Microscopiquement, les photonsc incidents (en vert Fig. 1 (c)) qui possèdent une énergie \( h\nu_0 \) , interagissent avec les molécules de deux manières. Ils peuvent interagir sans échanger d’énergie avec les molécules, on parle alors de diffusion élastique. Mais ils peuvent également interagir en leur fournissant l’énergie nécessaire pour faire passer les molécules dans un état de vibration excité (Fig. 1 (c)), ces dernières se mettent alors à vibrer et les photons incidents repartent avec une énergie inférieure à \( h\nu_0 \) . En analysant la lumière provenant de l’échantillon on détecte ainsi des photons ayant une énergie plus faible que \( h\nu_0 \) (photons orange et rouge d’énergie \( h\nu_1, h\nu_2 < h\nu_0 \) Fig. 1 (c)) ce qui se traduit dans le spectre par des pics décalés en énergie par rapport à l’énergie \( h\nu_0 \) . Ainsi à un état de vibration de la molécule va correspondre un pic dans le spectre Raman. Chaque molécule possédant des modes de vibrations caractéristiques, de tels spectres constituent une véritable carte d’identité propre à la molécule sondée.
De manière générale toutes les spectroscopies vibrationnelles reposent sur le même principe : les molécules sont excitées optiquement par des photons qui servent de sonde, qu’on appelle souvent photons-sondes et les photons issus de l’interaction sont collectés et analysés afin d’établir un spectre. Comme la molécule possède une longueur de l’ordre du nanomètre et le photon une longueur d’onde de l’ordre de la centaine de nanomètre, du point de vue de ce dernier la molécule est vue comme un objet ponctuel sans dimensions. Le spectre optique d’une molécule est donc la carte d’identité d’un objet sans dimension.
Mais si nous disposions d’une sonde suffisamment petite pour venir sonder à différents endroits de la molécule, que deviendrait alors son spectre optique ? C’est la question à laquelle nous avons tenté de répondre dans nos expériences. Pour cela il nous a fallu trouver une sonde bien plus petite qu’un photon et idéalement bien plus petite qu’une molécule …
Des électrons pour imager et obtenir un spectre optique.
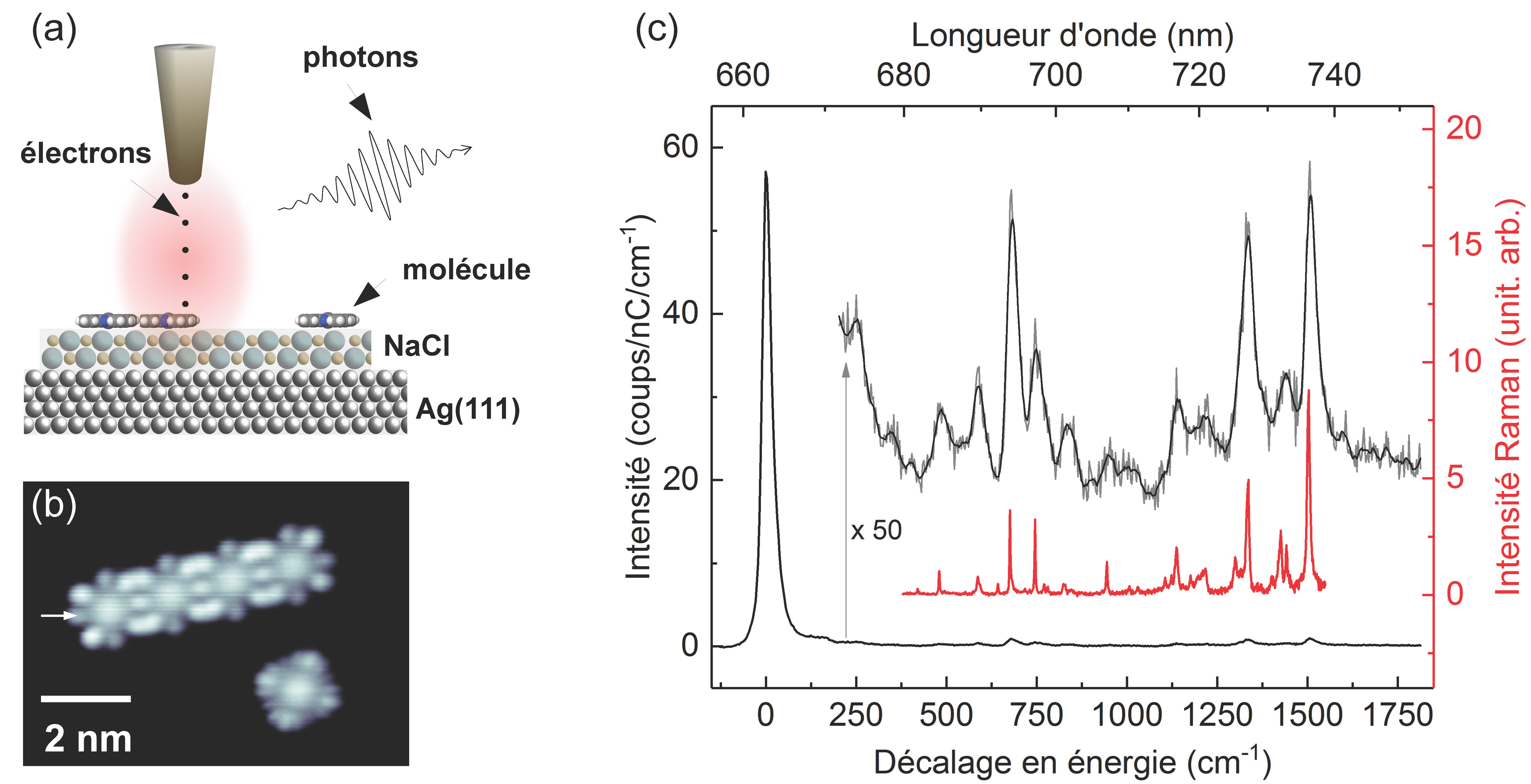
Lorsque l’on pense à une particule beaucoup plus petite qu’une molécule, on pense tout de suite aux électrons. Dans nos expériences, dont les résultats ont été publiés récemment [1], nous avons remplacé l’excitation optique par une excitation électrique. Pour cela nous avons utilisé un microscope à effet tunnel (STM) qui, grâce à une pointe extrêmement fine, permet de topographier et de manipuler les molécules individuellement (Fig. 2 (b))d. En injectant directement à partir de cette pointe les électrons à l’intérieur même des molécules (Fig.2 (a)), certains électrons peuvent transférer de l’énergie à la molécule. La molécule passe alors dans un état excité et se desexcite en émettant un photon. La lumière émise est ainsi collectée et analysée afin d’établir un spectre. En appliquant ce protocole à des molécule de phtalocyanine de zinc (celle représentée fig. 1), nous avons obtenu des spectres très similaires à ce qu’on peut obtenir en spectroscopie Raman (Fig.2 (c)). Un spectre optique, c’est à dire une carte d’identité de la molécule, est alors obtenu sans avoir recours à une excitation lumineuse.
Grace au STM il est ainsi possible d’imager mais également d’obtenir un spectre optique avec une résolution spatiale bien au delà de ce qu’il est possible de réaliser avec des techniques optiques conventionnelles.
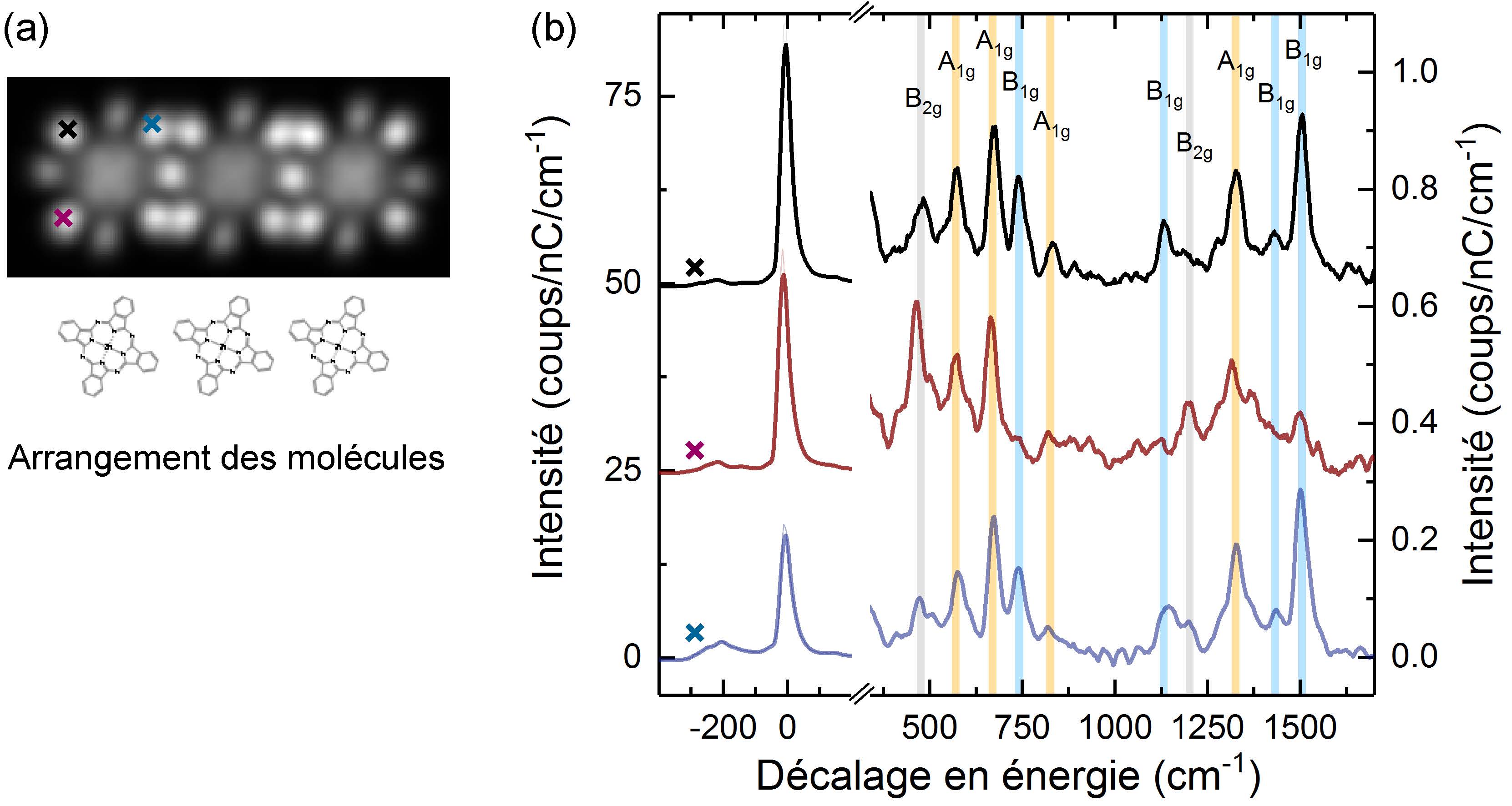
Maintenant, que se passe-t-il lorsque l’on sonde différentes sous-structures de la molécule ? Pour répondre à cette question nous avons réalisé une excitation électrique en différents endroits d’une molécule (croix de couleurs Fig.3 (a)). Les spectres correspondants sont donnés Fig.3 (b). On observe que les spectres varient de manière très nette selon l’endroit où est réalisée l’excitation ; en d’autres termes la carte d’identité de la molécule varie selon la zone sondée au sein de la molécule. Ce résultat nouveau permet d’envisager la spectroscopie optique sous un autre angle. Lorsque la molécule n’est plus considérée comme un objet ponctuel, sa carte d’identité n’est plus donnée par un seul spectre optique, mais par l’ensemble des spectres obtenus en chaque point de la molécule. Cela ouvre la voie à des questions passionnantes sur la vision que nous avons du spectre optique d’une molécule.
Nos résultats suggèrent également que cette variation à l’intérieur même de la molécule, provient de la symétrie des modes de vibrations sondés. En effet des modes de vibrations de même symétrie (c’est le sens des termes \(A_{1g}\), \(B_{1g}\) et \(B_{2g}\)) correspondent à des pics dans le spectre ayant des dépendances spatiales similaires (voir la partie « Quelques explications techniques » pour plus de détails).
Vers un nouveau type de nano-spectroscopie ?
Dans ces expériences nous avons montré qu’il était possible d’utiliser les électrons comme sonde pour obtenir une carte d’identité optique de la molécule sondée. Notre source d’excitation étant très précise nous avons pu montrer que ce spectre optique dépendait de l’endroit où était réalisée l’excitation. La carte d’identité d’une molécule est ainsi donnée par l’ensemble des spectres acquis à chaque endroit de la molécule et non plus par un unique spectre. Ces résultats permettent d’imaginer un nouveau type de nano-spectroscopie résolue à l’échelle submoléculaire, un outil permettant d’étudier la matière à des échelles qui jusqu’ici n’étaient pas accessible aux techniques optiques généralement utilisées.
D’autres expériences sont prévues sur d’autres molécules afin de confirmer nos résultats. Plus fondamentalement nous envisageons des expériences où il serait possible de comparer, sur la même molécule, une excitation par des photons et une excitation par des électrons. Ce type d’expérience permettrait de mieux comprendre les mécanismes de transfert d’énergie entre les électrons et les molécules, car ces mécanismes sont encore mal compris.
Quelques explications techniques
Symétrie d’un mode de vibration d’une molécule
Dans notre article [1], nous avons relié la symétrie des modes de vibration de la molécule à la dépendance en intensité des pics correspondants. Pour bien comprendre cette idée de symétrie examinons le cas d’une molécule plus simple que la molécule de phtalocyanine de zinc, par exemple le dioxyde de carbone CO2. La figure 4 représente deux de ses quatre modes de vibration. Dans le premier mode (Fig. 4 (a)) les deux liaisons se raccourcissent et s’allongent en même temps. On dit donc de ce mode de vibration qu’il est symétrique. Dans le deuxième mode (Fig. 4 (b)), une liaison s’allonge pendant que l’autre se raccourcit, et vice-versa. On dit donc de ce mode de vibration qu’il est anti-symétrique.
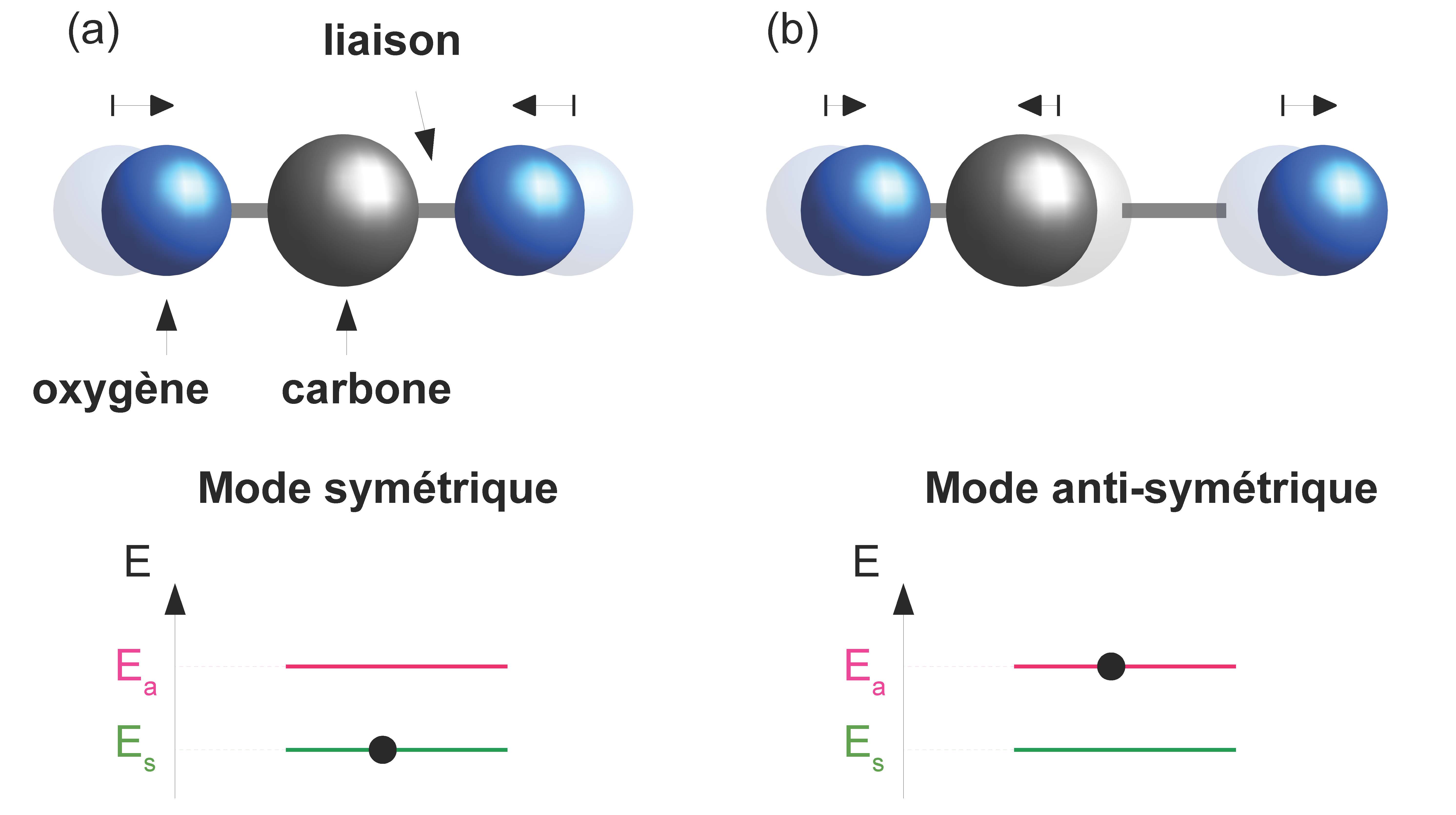
Pour une molécule plus complexe, il existe une multitude d’éléments (axes, plans …) par rapport auxquels on peut définir une symétrie. Il existe donc une multitude de modes symétriques ou anti-symétriques par rapport à ces éléments. Pour les répertorier on utilise une nomenclature qui contient l’information sur la symétrie du mode concerné, c’est le sens de \(A_{1g}\), \(B_{1g}\) et \(B_{2g}\) dans l’article (on parle de représentation irréductible).
Fonctionnement d’un microscope à effet tunnel
Nos travaux utilisent un microscope à effet tunnel (STM en anglais pour Scanning Tunneling
Microscope) qui permet d’injecter de manière très précise des électrons à l’intérieur d’une molécule. Initialement, le STM a été conçu pour réaliser des topographies de surfaces conductrices avec une résolution atomique. Son principe est décrit en figure 5. Un STM est constitué d’une pointe métallique et d’une surface conductrice séparées d’une distance \( z \) de l’ordre de 1 nm (Fig. 5 (a)) et entre lesquelles on applique une tension \( V \) de l’ordre de 1 V. Tout un système composé de tubes piézo-électriques e permet de déplacer de manière contrôlée la pointe par rapport à la surface.
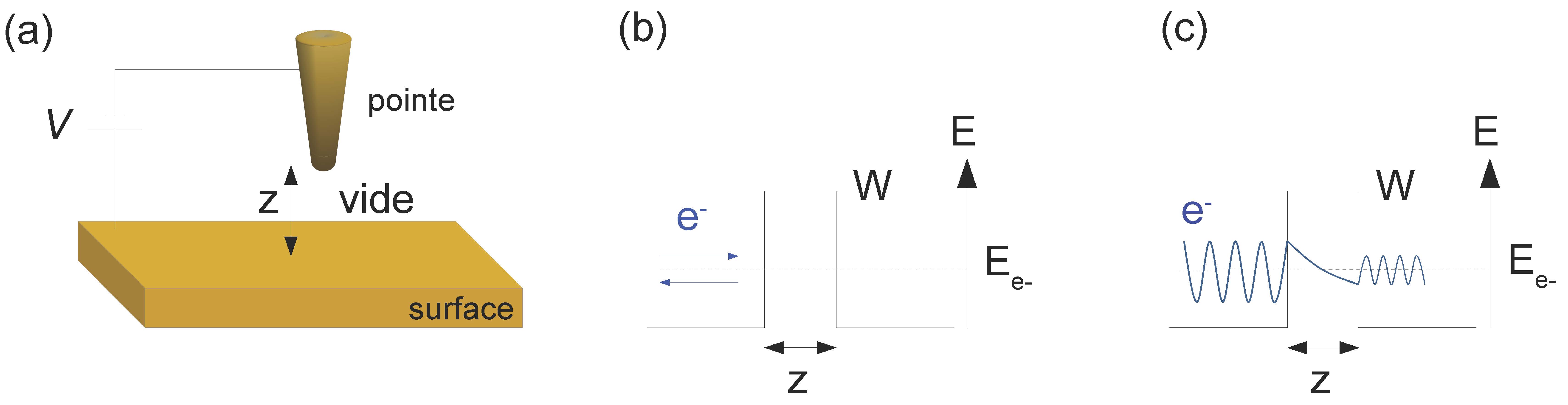
Intéressons nous maintenant à ce qu’il se passe au niveau de la pointe et de la surface. Si on adopte un point de vue classique (Fig. 5 (b)), où la physique est régie par les lois de Newton, il ne peut pas y avoir de courant électrique. En effet les électrons ne peuvent franchir la barrière de potentiel (d’énergie \( V \)) constituée par le vide car leur énergie n’est pas suffisante (\( E_{e^-}<W \)). Les électrons ne peuvent pas passer de la pointe à la surface.
Mais en réalité le monde à cette échelle est régi par les lois de la physique quantique et les objets peuvent se comporter comme des ondes ou comme des particules. Ainsi, l’onde de probabilité associée à l’électron n’est pas totalement stoppée par la barrière, elle est simplement amortie et elle peut même être transmise au delà de la barrière (Fig. 5 (c)). Ainsi, il y a une certaine probabilité pour que l’électron passe quand même de la pointe à la surface, c’est ce qu’on appelle l’effet tunnel, ce qui donne lieu à l’apparition d’un courant dit courant tunnel. L’onde s’amortit dans la barrière de manière exponentielle avec la distance et sous certaines approximations la probabilité de transmission varie elle aussi de manière exponentielle. Grossièrement, on peut considérer que le courant tunnel varie comme \(I_{tunnel} \propto \exp (−Kz)\) où \(K\) est une constante dépendant du type de métal constituant les électrodes. Typiquement avec une pointe et une surface en argent (cas de nos expériences), si la distance \(z\) varie de 1 Å, le courant \(I_{tunnel}\) varie d’un facteur 10. Autrement dit une très faible variation de distance induit une très grande variation du courant. Ainsi, en mesurant le courant tunnel tout en balayant la surface il est possible d’obtenir une véritable topographie de la surface avec une résolution atomique. C’est le principe de base du STMf.
Notes
| a. | ↑ | Qui représente l’intensité des différentes longueurs d’onde de la lumière. |
| b. | ↑ | Dans nos expériences nous utilisons des molécules de phtalocyanine de zinc, une molécule très étudiée pour ses propriétés optiques. Elle est par exemple étudiée pour ses applications potentielles dans des cellules photo-voltaïque ou encore dans certaines thérapies contre le cancer. |
| c. | ↑ | La lumière peut être vue comme une onde mais aussi comme une assemblée de paquets d’énergie appelés photons. |
| d. | ↑ | Ces topographies sont en général appelées images STM. |
| e. | ↑ | Les matériaux piézo-électriques ont la capacité de se déformer lorsqu’on leur applique un champ électrique. En fixant une pointe sur de tels matériaux et en appliquant des champ électriques de manière contrôlée, il est ainsi possible de déplacer la pointe de manière extrêmement précise. |
| f. | ↑ | En pratique pour réaliser des topographies on utilise le STM en mode courant constant. Dans ce mode de fonctionnement, une électronique de régulation ajuste en continue la distance \(z\) pointe-surface pour garder le courant constant lorsque la pointe balaye la surface. Les variations de \(z\) sont enregistrées pour constituer une topographie de la surface. C’est de cette manière que les topographies présentées dans cet article ont été réalisées (voir Fig. 2 et 3). |