La mécanique du tricot

Mécanique et objets structurés

Comment se déforme un truc quand on tire dessus ? La branche des sciences qui essaie de répondre à cette question s’appelle la mécanique et se trouve à la frontière entre les mathématiques, la physique et l’ingénierie. Le genre de problèmes qui entrent dans cette catégorie sont extrêmement variés. Le « truc » en question peut être ou bien solide ou liquide et avec une taille allant de l’aile d’avion à la cellule vivante. Quant à la déformation, elle peut être accompagnée d’autres phénomènes, comme une fracture ou un changement de température, et il y a aussi plein de manières de « tirer » sur un objet.

Ces problèmes sont souvent complexes et proches d’applications directes, ce qui fait de la mécanique un domaine qui suscite énormément d’intérêts autant d’un point de vue industriel que pour les sciences fondamentales. Un sujet particulièrement actif ces dernières années est l’étude de matériaux pour lesquels les propriétés mécaniques découlent plus de la structure qui leur est imposée que du matériau de départ. Ces objets structurés, aussi appelés « métamatériaux », sont susceptibles d’acquérir des propriétés inédites par rapport à des matériaux plus standards, mais aussi des réponses ajustables à des besoins spécifiques. En revanche, il y a un prix à payer: leurs comportements mécaniques sont particulièrement difficiles à prédire.

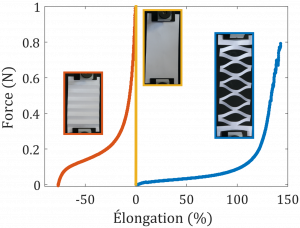
Un exemple qui focalise beaucoup d’attention actuellement consiste à prendre un objet quasiment bidimensionnel, comme une feuille de papier, et à y ajouter une structure en imposant un réseau de plis (origami ¹) ou de coupures (kirigami ²). Par ces simples structurations, les propriétés mécaniques, comme la déformabilité quand on tire dessus, varient drastiquement de la feuille intacte (voir la figure en annexe). Ces propriétés intéressent les ingénieurs, en aérospatial par exemple ³, pour les applications que ces méthodes ouvrent, mais aussi les physiciens car cela pose des questions plus fondamentales sur les interactions entre structure et matière ⁴.

Tricoter n’est pas tisser

Que vient alors faire le tricot dans tout ça ? Et bien le tricot, ou même les textiles en général, ne sont que des fils structurés par des entrelacements : un textile rentre donc parfaitement dans la catégorie des matériaux structurés. L’avantage avec les textiles c’est que pour illustrer l’effet de la structure sur les propriétés mécaniques de l’objet, il suffit de prendre des objets qui traînent autour de nous. Un tricot et un tissu, par exemple, n’ont pas du tout la même structure et on peut facilement se rendre compte que la réponse mécanique qui en résulte est aussi différente. Prenez par exemple une écharpe (ou une chaussette, généralement tricotée), un chiffon (généralement tissé, votre jean fait aussi l’affaire) et un fil tout simple. En tirant légèrement sur chacun de ces objets, on s’aperçoit que le fil et le chiffon ne se déforment quasiment pas alors que l’écharpe s’allonge facilement de presque deux fois sa taille. Ces différentes réponses persistent si la nature du fil change, notamment si le tricot et le tissu sont composés du même fil. La structure des entrelacements du fil joue par conséquent un rôle prédominant, devant les propriétés du fil en lui-même.

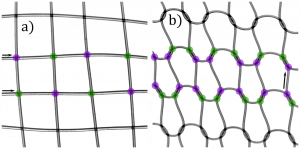
Pour interpréter ces résultats il faut donc se pencher sur la structure fine de ces textiles. Un tissu est composé de deux groupes de fils rectilignes qui viennent s’entrecroiser alternativement à angle droit (Figure 1.a) Lorsque l’on vient tirer dessus, on tire directement dans la longueur des fils, la réponse mécanique d’un tissu n’est donc pas très différente de celle d’un fil simple, c’est-à-dire proche de l’inextensibilité. Un tricot en revanche est constitué d’un seul fil qui est arrangé sous la forme d’un réseau périodique de boucles appelées mailles (Figure 1.b). Tirer sur un tricot revient de ce fait, non pas à tirer sur un fil, mais à déformer des boucles. Les fils étant des objets fins, il est bien plus aisé de les fléchir que d’en changer la longueur. Prenez par exemple n’importe quel câble d’alimentation, l’allonger en tirant dessus est assez éprouvant, mais si vous formez une boucle avec ce fil, déformer cette boucle devient alors un jeu d’enfant. C’est ce mécanisme, induit par les différents agencements des croisements, qui permet d’expliquer la différence de réponse mécanique entre un tissu et un tricot.

Une fois que l’on a compris qualitativement comment se déforme un tricot (c’est-à-dire identifié les mécanismes en jeu), on va maintenant construire un modèle pour prédire quantitativement sa réponse mécanique (c’est-à-dire mettre le problème en équations pour pouvoir comparer les résultats du modèle à ceux d’expériences).

Une approche « à la physicienne »

Mettre cette mécanique du tricot en équations permet, en plus de pouvoir donner des prédictions, de démêler le rôle des paramètres qui proviennent du matériau de ceux qui viennent de la structure. Les tricots revêtant une grande importance industrielle, ils ont déjà fait l’objet de nombreuses études pour les décrire et comprendre leur comportement mécanique. Les différentes approches peuvent être séparées grossièrement en deux catégories. Une première consiste à détailler avec des équations la trajectoire et les déformations au niveau du fil ⁵. De par la complexité de ces équations et la difficulté à traduire l’effet des croisements, cette méthode est restreinte à la description d’une courte portion du fil et non du tricot dans son ensemble. La seconde approche, poussée par la communauté d’animation graphique, est intégralement numérique et permet de décrire des tricots entiers dans de nombreuses et complexes situations ⁶. En revanche, on perd la compréhension des relations entre structure et mécanique sous-jacentes car le code numérique joue le rôle d’une « boîte noire » qui masque le fonctionnement du système.

L’idée de départ de ma thèse était de revisiter l’étude du tricot avec une approche plus « physicienne », c’est-à-dire de simplifier suffisamment le système pour ne garder que l’essentiel et ainsi pouvoir expliciter comment émergent les propriétés mécaniques. Simplifier un tricot signifie laisser de côté son écharpe en laine, et partir d’un fil dont on connaît parfaitement les propriétés (ici du fil de pêche en nylon), garder la même structure pour chaque maille (pas de motifs fantaisistes) et séparer les échelles de longueur. Il y a trois longueurs caractéristiques qui apparaissent dans un tricot : le diamètre du fil, la distance entre deux boucles voisines et la taille du tricot. Séparer ces dimensions revient à faire en sorte que chaque longueur soit au moins 10 fois plus petite que la suivante. Cette séparation, en plus de permettre une meilleure visualisation, simplifie significativement la résolution du problème. Ensuite, pour prendre en compte directement la structure du tricot dans sa description, le système est décrit à une échelle intermédiaire entre le fil et le tricot entier, c’est-à-dire à l’échelle des mailles.

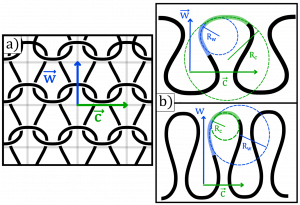
Le tricot est donc vu comme un réseau périodique de boucles et qui constitueront nos briques élémentaires. Chaque boucle du réseau est caractérisée par deux vecteurs, \( \overrightarrow{c}\) et \( \overrightarrow{w}\), qui la relient respectivement à sa voisine de droite et à celle du dessus (Figure 2.a). Ces vecteurs sont définis pour chaque maille du tricot et leurs longueurs traduisent la taille de cette maille. Les mailles pouvant avoir des tailles différentes selon la déformation que subit le tricot, ce sont donc des champs de vecteurs qui dépendent de la position de la boucle dans le tricot.

Énergie et contraintes

Maintenant que l’on a choisi une manière de représenter notre tricot, décrire sa mécanique consiste à déterminer comment son énergie élastique varie lorsqu’on le déforme. Un système va toujours favoriser le mode de déformation qui lui coûte le moins d’énergie, or on a vu que pour un fil, se courber est bien plus facile que de s’allonger. On va donc faire l’hypothèse que lorsque le tricot se déforme, le fil des boucles va simplement changer sa courbure tout en gardant une longueur constante. Cette hypothèse est valable seulement si le fil est courbé sur une distance qui reste grande devant son diamètre, ce qui revient à tricoter un fil dont le diamètre est bien plus petit que la distance entre les mailles, comme c’est le cas pour notre tricot de la Figure 1.b. Il ne reste donc plus qu’à exprimer, au sein d’une maille, l’énergie de flexion du fil et son inextensibilité en fonction de notre description en \( \overrightarrow{w} \) et \( \overrightarrow{c} \).

Une manière de quantifier la courbure d’un fil passe par ce que l’on appelle son rayon de courbure \(R\), qui est défini par le rayon du cercle qui suit localement la même courbure que le fil (Figure 2.b). Une portion de fil de longueur \(dl\) porte alors une énergie de courbure de \(B dl / R^2 \), avec \(B\) une quantité intrinsèque au fil appelée module de flexion. Ce module dépend de deux paramètres : la rigidité du matériau constituant le fil, connue sous le nom de module d’Young, mais aussi du diamètre du fil (plus le diamètre d’un fil est gros, plus il est difficile à courber). Cette formule nous indique que plus le fil est courbé (rayon de courbure associé petit), plus le fil emmagasine de l’énergie. Un fil va donc toujours tendre à maximiser son rayon de courbure.

Dans notre tricot, la taille maximale de ce rayon est limitée par les dimensions de la maille donnée par la norme des vecteurs \( \overrightarrow{c} \) et \( \overrightarrow{w} \). En effet, si la taille de la maille diminue dans une direction, le rayon de courbure du fil dans cette même direction va être forcé de diminuer (Figure 2.b). Grâce à cette première observation il est possible d’écrire l’énergie d’une maille en fonction de nos vecteurs \( \overrightarrow{c} \) et \( \overrightarrow{w} \). L’énergie élastique que porte une maille est donc directement liée à sa structure en forme de boucle.

Cependant, connaître l’énergie du tricot ne suffit pas car, avec seulement cet ingrédient, les mailles grossiraient indéfiniment pour augmenter le rayon de courbure du fil et ainsi minimiser son énergie élastique. En revanche, grossir une maille dans toutes les directions implique forcément d’augmenter aussi la longueur de fil, or notre fil est inextensible. Cette contrainte impose donc que, si une maille s’allonge dans une direction, elle doit rétrécir dans une autre, une contrainte qui s’écrit naturellement en fonction de \( \overrightarrow{c} \) et \( \overrightarrow{w} \). Même si les détails ne sont pas explicités ici, ces deux ingrédients sont suffisants pour décrire la mécanique d’une maille.

Mais est-ce que ça marche ?

Écrire un modèle c’est bien, vérifier qu’il décrit correctement des expériences c’est mieux. Pour commencer, on considère le cas le plus simple où toutes les mailles du tricot se déforment de la même manière. Pour cela on vient tirer sur le tricot dans une direction, ici celle de \( \overrightarrow{w} \), et on laisse les mailles rétrécir autant qu’elles veulent dans la direction orthogonale \( \overrightarrow{c} \).

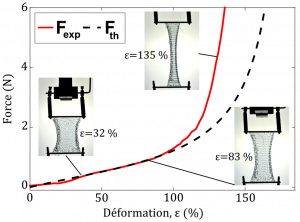
Toutes les mailles subissent la même déformation et on en profite pour mesurer quelle force est nécessaire à cette élongation (Figure 3). La hauteur initiale des mailles est notée \(w_0\) , et on définit la déformation \(ε = (w – w_0)/w_0\), comme la différence relative entre la hauteur imposée et celle initiale. En comparant la réponse expérimentale à celle prédite théoriquement, les deux coïncident jusqu’à \(ε = 100\)%, ce qui équivaut à un allongement de deux fois la taille initiale. Le modèle, aussi simple soit-il, parvient à rendre compte de la mécanique du tricot dans cette configuration. La formule mathématique de la prédiction permet aussi d’extraire une rigidité effective du tricot qui est proportionnelle à \(B / c_0 w_0\).

Ce résultat montre que la rigidité d’un tricot dépend à la fois des propriétés du fil utilisé (\(B\)) mais aussi de propriétés purement structurelles comme la taille initiale des mailles ( \(c_0\) et \(w_0\)). Notre modèle a aussi ses limites, pour \(ε >100\)%, la force nécessaire pour déformer le tricot devient beaucoup plus importante que celle prédite. On peut toutefois comprendre pourquoi en observant la photographie correspondant à cette partie. On remarque en effet que les mailles sont tellement allongées que la séparation d’échelle entre le diamètre du fil et son rayon de courbure n’a plus lieu d’être. Le fil n’est alors plus seulement fléchi, mais aussi étiré et compressé, ce qui sort du cadre de description de notre modèle.

Pour prédire des modes de déformation du tricot plus compliqués, notamment où toutes les mailles ne se déforment pas de la même manière, la même approche peut toujours être utilisée. Il faut toutefois ajouter une contrainte supplémentaire qui relie les déformations d’une maille à ses voisines et utiliser une méthode mathématique, appelée Lagrangienne, un peu plus compliquée. Cette méthode permet de trouver les équations différentielles que \( \overrightarrow{c} \) et \( \overrightarrow{w}\) doivent satisfaire pour minimiser l’énergie totale du tricot tout en satisfaisant la contrainte d’inextensibilité du fil. Pour de plus amples détails, les lecteurs intéressés peuvent jeter un œil à notre article ⁷.

Conclusion

En dépit de leur aspect anodin, les textiles, et le tricot en particulier, constituent un terrain de jeu très riche pour l’étude des matériaux structurés. Les questions soulevées relèvent à la fois de la physique fondamentale tout en restant proche d’applications (renforts de matériaux composites, « soft robots »).  En effet, en partant d’un objet quasiment le plus simple qu’il soit, un fil, on peut le structurer de nombreuses manières différentes pour obtenir une fantastique diversité de formes et de réponses mécaniques. On peut même faire le parallèle entre la réponse mécanique d’un tricot et celle d’autres systèmes qui, au premier abord, semblent très éloignés. Par exemple, en regardant de près le bruit de la réponse mécanique causée par le frottement aux points de contacts du fil, on a pu mettre en évidence une dynamique qui prend la forme d’«avalanche» que  l’on retrouve dans la déformation de milieux granulaires ou même des tremblements de terre (dynamique aussi connue sous le nom de loi de Gutenberg-Richter) ⁸.