
L’Univers constitue une sorte de « laboratoire géant » qui permet aux physiciens d’étudier leurs théories à des échelles complètement inaccessibles sur Terre. En particulier, les premiers instants de l’Univers correspondent à des énergies titanesques dont les traces nous donnent des informations difficilement accessibles autrement. Dans ce billet, nous allons voir comment les particules les moins bien comprises du Modèle Standard, les neutrinos, jouent un rôle important dans la dynamique des premières secondes de l’Univers. On peut alors utiliser des télescopes pour comprendre un peu mieux comment se comportent ces particules… élémentaires !
Introduction : neutrinos et expansion de l’Univers
Les neutrinos sont des particules élémentaires (de même que les électrons \( e^{-} \), les photons \( \gamma \) ou les quarks \( q \)), dont voici la carte d’identité :
| Charge électrique | Masse | Nombre d’espèces | Interactions |
| 0 | Presque nulle (mais pas tout à fait) | 3 \( \nu_e \), \( \nu_\mu \), \( \nu_\tau \) et les antineutrinos associés | Force « faible » uniquement |
Comme son nom l’indique, la force faible à travers laquelle les neutrinos interagissent avec leur milieu est… faible. Si faible que les neutrinos sont très difficiles à détecter car ils traversent tout sans que cela les dérange. Historiquement, leur existence n’a été déduite qu’indirectement, parce que des réactions de désintégration radioactive ne semblaient pas respecter la conservation de l’énergie (cf. Annexe A). Les antineutrinos sont les antiparticules associées aux neutrinos. De manière générale, une antiparticule a la même masse et le même spin *, mais une charge électrique opposée à la particule associée. On reparlera plus bas de « l’antiélectron », couramment appelé positron \( e^{+} \). On a longtemps cru que les neutrinos étaient sans masse, mais le phénomène d’oscillations de neutrinos (cf. Annexe B) ne peut s’expliquer qu’avec des neutrinos massifs. Le mécanisme à l’origine de ces masses reste inconnu aujourd’hui.
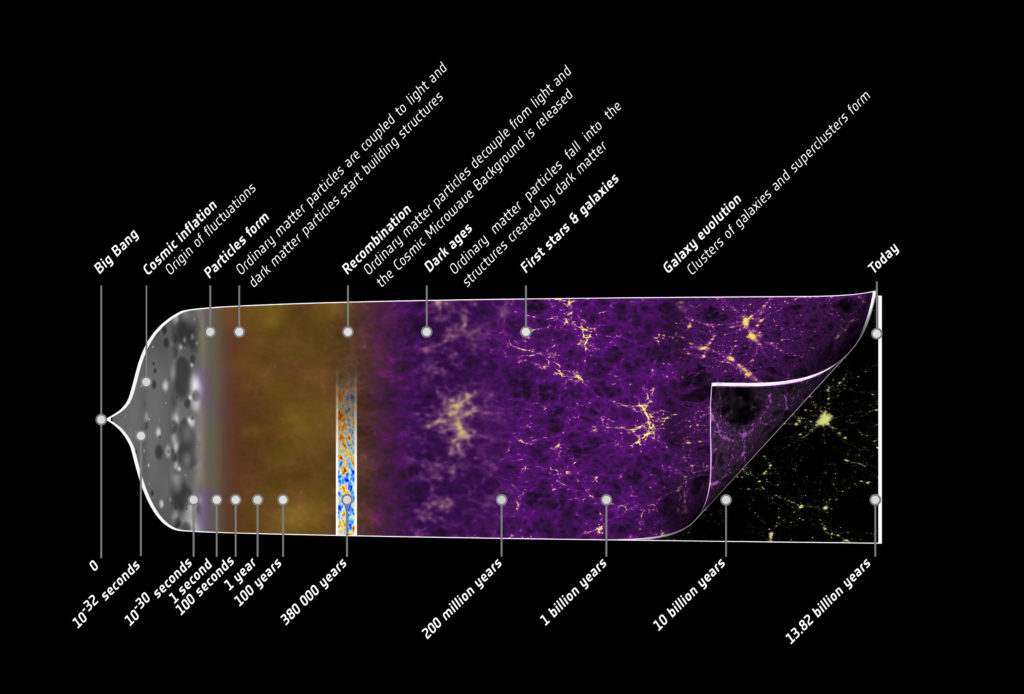
L’histoire de l’Univers se résume somme toute simplement : il est en expansion et se refroidit. Le refroidissement est une conséquence de l’expansion, puisque l’énergie contenue dans l’Univers se dilue — ce qui est donc associé à une diminution de la température. Cette évolution de l’Univers est décrite par le « modèle cosmologique standard », plus couramment dénommé « modèle du Big Bang ». L’hypothèse fondamentale de ce modèle est qu’initialement, l’Univers était infiniment dense et infiniment chaud. La gravité, qui façonne l’Univers aux grandes échelles, est supposée décrite par la théorie de la relativité générale : les équations montrent alors que l’énergie contenue dans l’Univers provoque l’expansion de l’espace-temps. On ne détaillera pas ici les composantes de ce modèle, présentées dans l’Annexe 1 de l’article de Jean-Baptiste.
Découplage et annihilations
Initialement, l’Univers est une « soupe » homogène de particules, à l’équilibre thermique. Au fur et à mesure que la température de l’Univers diminue, les choses changent peu à peu. Ici, nous allons nous intéresser à deux phénomènes.
1) Le découplage
Prenons l’exemple des neutrinos. À l’époque qui nous intéresse (température d’environ \( 10^{10} \mathrm{K} \), quelques secondes après le Big Bang), les particules les plus abondantes dans l’Univers sont les photons, les neutrinos et antineutrinos, ainsi que les électrons et positrons. Les différentes interactions entre ces particules permettent de maintenir l’équilibre (on dit que les espèces sont « couplées »)… sauf si l’expansion est trop rapide. On peut en effet comparer deux quantités : le taux d’interaction des neutrinos \( \Gamma \) (i.e., le nombre de collisions par seconde, ces collisions permettant aux différentes espèces de rester à la même température), et le taux d’expansion de l’Univers \( H \) (qui décrit comment les particules s’éloignent les unes des autres du fait de la dilatation de l’espace). Si \( \Gamma < H \), les interactions sont trop faibles pour maintenir l’équilibre thermique entre particules, celles-ci « s’éloignent trop vite ». Or, on l’a dit précédemment, les neutrinos n’interagissent que par la force « faible »… On montre précisément que pour des températures inférieures à \( T_\mathrm{dec} \simeq 10^{10} \mathrm{K} \), les neutrinos n’interagissent plus assez avec les autres particules pour rester à l’équilibre. On dit qu’ils se découplent†. Cela signifie que, la température continuant à diminuer, les neutrinos n’interagissent plus avec les autres particules ; ils « vivent leur vie » sans se soucier des photons, électrons et positrons environnants.
2) Les annihilations
Nous avons parlé des interactions qui maintiennent les particules à l’équilibre, mais quelles sont-elles ? Par exemple pour les électrons et positrons, une réaction très importante est
\( e^{-} + e^{+} \leftrightarrow \gamma + \gamma \)
De la gauche vers la droite, un électron et un positron s’annihilent pour former deux photons. Dans l’autre sens, deux photons donnent naissance à une paire électron-positron. Cette création de paire demande une certaine énergie : par leur existence même, les électrons et positrons possèdent une énergie dite « de masse » égale à \( m_\mathrm{e}c^2 \) (c’est la célébrissime formule d’Einstein \( E = m c^2 \)). Pour former l’électron et le positron, les photons doivent donc posséder, au moins, une énergie totale supérieure à \( 2m_\mathrm{e}c^2 \). Or, pour des espèces à l’équilibre thermique à la température \( T \), leur énergie moyenne est donnée par l’énergie thermique \( k_\mathrm{B} T \) (où \( k_\mathrm{B} \) est la constante de Boltzmann). Autrement dit, lorsque la température \( T \) est telle que \( k_\mathrm{B} T < m_\mathrm{e} c^2 \), il n’y a plus assez d’énergie en moyenne pour créer des paires \( e^{\pm} \): les électrons et positrons ne font que s’annihiler et disparaissent quasi-complètement‡. Numériquement, la température en-dessous de laquelle les électrons et positrons disparaissent est \( T_\mathrm{ann} = \frac{m_\mathrm{e}c^2}{k_\mathrm{B}} \simeq 0.6 \times 10^{10} \mathrm{K} \).
L’énergie issue de ces annihilations est transférée aux photons, qui se refroidissent donc comparativement moins vite que les neutrinos qui se sont découplés (et qui donc ignorent complètement ces annihilations). On montre alors que le ratio entre la température des photons et des neutrinos devrait valoir
\( \frac{T_\gamma}{T_\nu} = \left ( \frac{11}{4} \right )^{1/3} \simeq 1.40 \) (1)
Découplage incomplet des neutrinos
Toute cette histoire est bien jolie… mais elle est inexacte. On remarque que \( T_\mathrm{dec} \) et \( T_\mathrm{ann} \) sont très proches, de sorte que les neutrinos ne sont pas complètement découplés lorsque les annihilations \( e^{-}e^{+} \) se produisent. Cela se traduit par un (léger) transfert d’énergie vers les neutrinos, que l’on paramétrise historiquement par le nombre effectif de neutrinos \( N_\mathrm{eff} \). Il quantifie la densité d’énergie que possèdent les neutrinos (c’est-à-dire l’énergie par unité de volume, une quantité importante puisqu’elle influe sur le taux d’expansion de l’Univers). La densité d’énergie étant proportionnelle à la température puissance 4, on peut écrire \( N_\mathrm{eff} \) en fonction des températures des différentes espèces de neutrinos \( T_{{\nu}_{e,\mu,\tau}} \) :
\( N_\mathrm{eff} = \left ( \frac{11}{4} \right ) ^{4/3} \times \left [\left ( \frac{T_{\nu_e}}{T_\gamma} \right )^4 +\left ( \frac{T_{\nu_\mu}}{T_\gamma} \right )^4 + \left ( \frac{T_{\nu_\tau}}{T_\gamma} \right )^4 \right ] \)
Si les neutrinos étaient complètement découplés au moment des annihilations \( e^{-}e^{+} \), le ratio des températures serait donné par l’équation 1 et on aurait \( N_\mathrm{eff} = 3 \). Du fait du réchauffage partiel des neutrinos en réalité, on s’attend à avoir \( N_\mathrm{eff} > 3 \). Ce paramètre décrit donc combien d’espèces de neutrinos parfaitement découplés il faudrait avoir pour obtenir la vraie densité d’énergie observée.
Prédire aussi précisément que possible la valeur de \( N_\mathrm{eff} \) est un travail entrepris depuis plus de deux décennies, qui nécessite de prendre en compte de nombreux phénomènes physiques :
- les collisions entre neutrinos et électrons/positrons, qui permettent le transfert d’énergie ;
- l’expansion de l’Univers qui dépend elle-même de l’énergie stockée par les neutrinos ;
- les oscillations de neutrinos, phénomène purement quantique qui permet aux neutrinos de changer de saveur a au cours du temps (un \( \nu_\mathrm{e} \) peut devenir, avec une probabilité non-nulle, un \( \nu_\mu \) ou un \( \nu_\tau \) ). On introduit ce concept dans l’Annexe B. Pour complexifier la chose, ces oscillations de saveur sont différentes en présence d’électrons.
Ce dernier point est le plus complexe à prendre en compte numériquement. Le traitement des collisions se fait classiquement grâce à une équation différentielle dite de Boltzmann ; la version prenant en compte les oscillations est appelée équation cinétique quantique. Dans le cadre de ma thèse à l’Institut d’Astrophysique de Paris sous la direction de Cyril Pitrou, nous avons présenté dans (travail en collaboration avec Cristina Volpe) la première détermination du nombre effectif de neutrinos \( N_\mathrm{eff} \) prenant en compte exactement les oscillations. Pour cela, nous avons développé un code numérique qui résout l’équation cinétique quantique sur toute la gamme de températures correspondant au découplage des neutrinos. Le résultat obtenu, confirmé par une équipe indépendante , est le suivant :
\( N_\mathrm{eff} = 3.0440 \) (2)
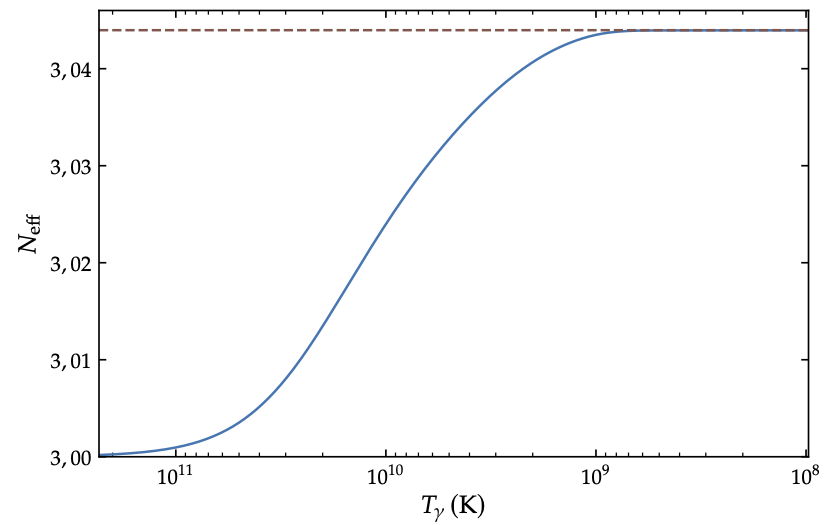
à une précision de quelques \( 10^{-4} \). Cette valeur est celle atteinte à la fin du découplage/réchauffage ; on représente en Figure 2 comment ce paramètre passe de 3 à 3,044 lors du découplage des neutrinos. Lorsque la température continue à diminuer, ce paramètre n’évolue plus et permet de décrire complètement la quantité d’énergie transportée par les neutrinos b.
Et les observations ?
Notre travail permet de comprendre comment les différents paramètres physiques affectent le découplage des neutrinos, et ouvre la voie à des études précises de théories allant au-delà du modèle standard des particules. Actuellement, les mesures expérimentales de \( N_\mathrm{eff} \) sont bien moins précises que le résultat (équation 2). C’est d’ailleurs souhaitable, puisque la valeur (équation 2) est une prédiction théorique qui sert notamment de base à d’autres analyses en cosmologie. Du fait de l’impact de l’énergie des neutrinos sur l’expansion de l’Univers, le satellite Planck, qui mesure le fond diffus cosmologique, peut contraindre la valeur de \( N_\mathrm{eff} \) comme étant :
\( N_\mathrm{eff} = 2.99 \pm 0.17 \)
valeur compatible avec 3 (qui correspondrait au découplage complet), et avec le résultat (équation 2), ce qui confirme qu’il existe bien a priori 3 espèces de neutrinos. De futures expériences (comme CMB-Stage 4) devraient atteindre une précision de l’ordre du pourcent. Étant donné la précision du résultat (équation 2), une différence avec une mesure expérimentale sera donc forcément le signe d’une nouvelle physique à découvrir.
Annexes
Annexe A : L’hypothèse du neutrino
L’existence des neutrinos a été initialement postulée afin de résoudre un problème assez « grave » pour les physiciens du début du XXe siècle. En effet, en étudiant des désintégrations radioactives comme par exemple celle du carbone 14 en azote, que l’on supposait alors être :
\( { }^{14}_6 C \rightarrow { }^{14}_{7} N + e^- \)
on trouvait que l’électron émis pouvait avoir toute une gamme d’énergies différentes, alors que la conservation de l’énergie prédisait une valeur très précise, à savoir \( \left ( m_{{ }^{14}C} – m_{{ }^{14}N} \right ) c^2 \).
La solution, proposée par Wolfgang Pauli en 1930 c, consista à supposer qu’une autre particule (le fameux neutrino) était émise en même temps que l’électron final, emportant une partie de l’énergie : en corrigeant la réaction précédente pour l’écrire \( { }^{14}_6 C \rightarrow { }^{14}_{7} N + e^- + \bar{\nu}_e \) (on sait désormais que c’est un antineutrino qui est émis), c’est la somme des énergies de l’électron et de l’antineutrino qui doit être égale à \( \left ( m_{{ }^{14}C} – m_{{ }^{14}N} c^2 \right ) \), d’où le fait que l’énergie de l’électron émis ne soit pas fixée. Pauli lui-même était assez mécontent de sa solution, car il pensait qu’une telle particule ne pourrait jamais être détectée§ … Un peu plus de deux décennies plus tard, en 1956, Cowan et Reines réalisèrent la première vérification expérimentale de l’existence du neutrino, confirmant la proposition de Pauli .
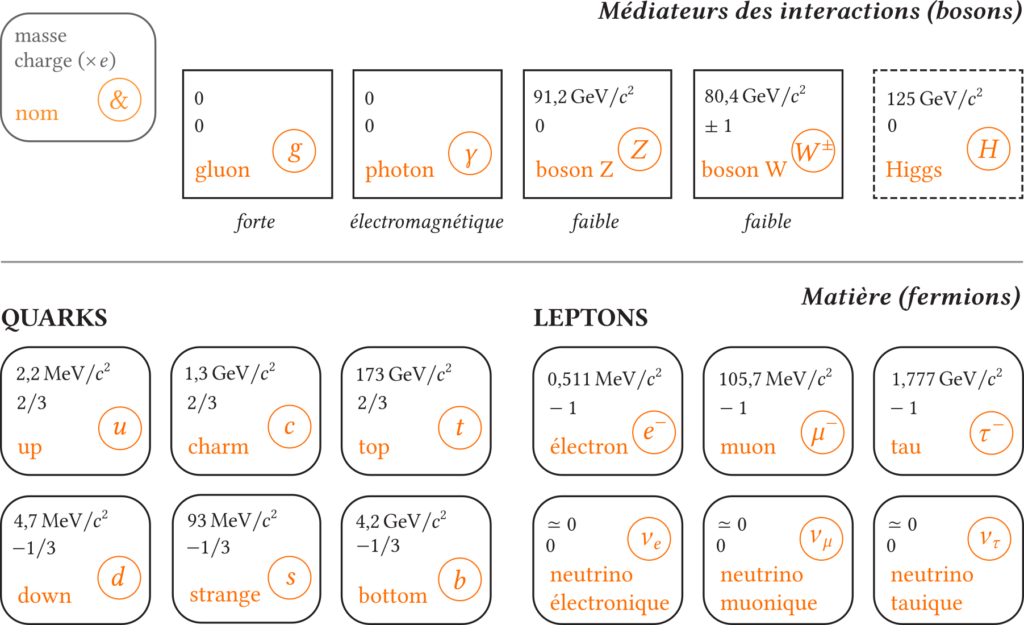
L’établissement théorique du Modèle Standard et les multiples confirmations expérimentales ont finalement permis de déterminer qu’il existe, selon le modèle actuel, trois espèces de neutrinos (électronique, muonique et tauique), ainsi que trois antiparticules associées. L’ensemble des particules du Modèle Standard ainsi que leurs propriétés sont résumés Figure 3.
Annexe B : Oscillations de saveur
Dans le Modèle Standard proprement dit, les neutrinos n’ont pas de masse. Cependant, on sait depuis la fin du XXe siècle que, si ces masses sont incroyablement plus faibles que celles de toutes les autres particules, elles ne peuvent pas être exactement nulles.
La première preuve est venue… du Soleil. Les astrophysiciens disposaient d’un modèle apparemment robuste des mécanismes à l’œuvre dans une étoile, qui prédisait notamment le rayonnement émis et les neutrinos qui vont avec. En 1970, l’expérience Homestake réalisa la première mesure du flux de neutrinos électroniques provenant du Soleil . La mesure donna un tiers de ce qui était prévu, une valeur confirmée par d’autres expériences ultérieures. Après de multiples théories et vérifications, l’explication qui passe tous les tests expérimentaux est la suivante : les neutrinos peuvent changer d’état de saveur au cours de leur propagation.
Ce n’est pas de la magie noire, mais un phénomène quantique bien connu qui se trouve intervenir en particulier pour les neutrinos.
Explication: En physique quantique, on décrit l’état d’un neutrino par un vecteur d’état. Une base de l’espace vectoriel des états est formée par l’ensemble \( \left \{ | \nu_e \rangle ,| \nu_\mu \rangle, |\nu_\tau \rangle \right \}\). Or, le Hamiltonien qui dicte l’évolution quantique de ces états dans le vide (ce qui décrit le trajet des neutrinos entre le Soleil et la Terre) n’est pas diagonal dans cette base. En effet, ce Hamiltonien se réduit à l’énergie totale des neutrinos, qui s’écrit :
\( E = \sqrt{p^2c^2 + m^2c^4} \simeq pc + \frac{m^2c^3}{2p} \).
Dans la théorie actuelle, les vecteurs d’état correspondant à des neutrinos de masse donnée (\( \left \{ | \nu_1 \rangle, | \nu_2 \rangle, | \nu_3 \rangle \right \} \), dits « états de masse ») sont différents des neutrinos de saveur donnée (« états de saveur »). La relation entre ces deux bases est donnée par la matrice PMNS U, de sorte que :
\( \begin{pmatrix} | \nu_e \rangle \\ | \nu_\mu \rangle \\ | \nu_\tau \rangle \end{pmatrix} = U \begin{pmatrix} | \nu_1 \rangle \\ | \nu_2 \rangle \\ | \nu_3 \rangle \end{pmatrix} \).
Ainsi, un neutrino produit dans l’état \( | \nu_e \rangle \), correspond à une superposition quantique d’états de masse. Comme les masses \( m_{1,2,3} \) sont différentes, ces états se propagent avec des phases différentes et, après une certaine distance, il y a une probabilité non-nulle de mesurer le neutrino dans un état de saveur différent. Pour un neutrino initialement dans l’état \( | \nu_e \rangle \), la probabilité de le mesurer dans chaque état de saveur après une certaine durée de propagation est représentée Figure 4.

Bibliographie
- *Le spin, propriété fondamentalement quantique, est aussi appelé « moment cinétique intrinsèque ».
- †La même chose se produit 380 000 ans plus tard lorsqu’il n’y a plus assez d’électrons pour que les photons restent couplés avec eux : ce découplage des photons donne naissance au fonds diffus cosmologique (voir la Figure. 1).
- ‡Il y a en réalité environ un milliardième de moins d’antimatière que de matière, d’où le fait que les annihilations aient conduit à un Univers qui semble uniquement composé de matière. L’origine de cette asymétrie est toujours inconnue.
- §Citons Pauli : “I have done a terrible thing today, something which no theoretical physicist should ever do. I have suggested something that can never be verified experimentally”.
Notes
| a. | ↑ | Hélas, ce terme ne désigne pas le goût prononcé de la soupe primordiale de l’Univers, mais simplement le type de particule. Rigoureusement, la saveur est une propriété importante au cœur de la théorie de l’interaction électrofaible, qui regroupe les particules en doublets du groupe spécial unitaire \( \textbf{SU}(2) \). Délicieux, non ? |
| b. | ↑ | Pour être tout à fait exact, cela n’est plus valable lorsque la masse des neutrinos (toujours inconnue) devient comparable à leur énergie cinétique. Toutefois, cela ne se produit que très tard dans l’histoire de l’Univers, et n’influe donc absolument pas sur les expériences qui permettent de déterminer \( N_\mathrm{eff} \). |
| c. | ↑ | Pauli adresse une lettre le 4 décembre 1930 à un groupe de physiciens nucléaires à Tübingen en Allemagne pour leur évoquer son “remède inespéré” permettant de sauver le principe de conservation de l’énergie. Une copie de la lettre est accessible dans l’Archive Pauli du CERN (https://cds.cern.ch/record/83282/files/meitner_0393.pdf) et une traduction est proposée sur le site LaRadioactivité (https://laradioactivite.com/le-phenomene/lettre-pauli). |








