Détection d’objets, reconnaissance de l’écriture, traduction automatique, l’apprentissage automatique est en train de bouleverser la technique moderne, et est aujourd’hui la pierre angulaire de l’intelligence artificielle. Certains outils de la physique peuvent aider à comprendre ces machines intelligentes, et il y a fort à parier que les deux domaines de recherche grandiront de l’étude de ces connexions.
La révolution de l’intelligence artificielle
Au cours des deux dernières décennies, l’intelligence artificielle a fait d’immenses progrès et ces succès sont en train de bouleverser notre rapport à l’informatique. Aujourd’hui, on ne s’étonne ni de la mise au point automatique de notre appareil photo sur les visages, ni de la pertinence des réponses automatiques proposées par notre serveur d’e-mail. Ce qui se cache derrière, c’est un ensemble des programmes informatiques qui permettent de faire accomplir à des ordinateurs ces tâches très complexes, dites intelligentes, telles que reconnaître un visage dans une vidéo ou tenir une conversation.
Dans cet article, nous aborderons d’abord les bases de l’apprentissage automatique, qui est un des principaux instruments de l’intelligence artificielle. Nous nous concentrerons ensuite sur une application, les modèles génératifs et en particuliers les machines de Boltzmann, qui empruntent des concepts à la physique.
Un apprentissage automatique
L’apprentissage automatique consiste créer des algorithmes capables d’apprendre à effectuer une tâche à partir d’un ensemble d’exemples. Imaginons que l’on souhaite trier des photos de chats et de chiens. On fournit d’abord à l’algorithme un ensemble d’images pour lesquelles la tâche désirée a été réalisée au préalable : le résultat (chat ou chien) pour chaque image est connu. Sur ces exemples, l’algorithme s’entraîne, pour ensuite savoir distinguer les deux catégories sur n’importe quelle nouvelle image. Ce qui est crucial dans cette méthode, c’est qu’on ne donne à l’algorithme que les photos d’entraînement, aucune information supplémentaire sur ce qui différencie un chat d’un chien, et qu’il parvient, in fine, à généraliser sur de nouvelles photos. D’où l’idée d’un apprentissage automatique.
Entrons un peu plus dans les détails, comment en pratique peut-on entraîner un algorithme ? La première étape est de définir une fonction avec beaucoup de paramètres, dont l’espace de départ est l’ensemble des photos de chat et de chien et dont l’espace d’arrivée est l’ensemble à deux éléments \( \{\)« chat », « chien »\(\} \). L’apprentissage consiste ensuite à ajuster les paramètres de cette fonction tel qu’elle associe à une image de chat la valeur « chat », et respectivement à une image de chien la valeur « chien ».
Sans le savoir, vous avez peut-être déjà utilisé l’un des modèles les plus simples de l’apprentissage automatique : la régression linéaire. À partir d’un ensemble de points d’entrainement \( (x,y) \in \mathbb{R}^2\) , vous avez ajusté les paramètres (\( a\) et \( b\)) d’une fonction affine \( y=f(x)=ax+b\). Ainsi vous avez pu prédire pour un nouvelle valeur de \(x \), la valeur de \( y\) correspondante.
Les deux exemples ci-dessus, la classification des chats et des chiens et la régression linéaire, sont des illustrations d’apprentissage dit supervisé. Ce type d’apprentissage consiste à apprendre la relation entre une entrée et une sortie. Dans nos exemples, une entrée correspond à une photo d’animal ou une valeur de \(x\) et une sortie correspond à une valeur « chat » ou « chien », ou une valeur de \(y\). On parle de supervision car on indique à l’algorithme pour une entrée donnée la bonne réponse, c’est-à-dire la valeur de sortie correspondante.
L’apprentissage non supervisé est un peu plus complexe. Il s’agit de découvrir automatiquement des structures dans une base de données, sans qu’il ne s’agisse ni de classifier ni de prédire un valeur de sortie. C’est ce qui va nous intéresser dans la suite de cet article.
Modélisation de lois de probabilités et modèle génératif
La modélisation de lois de probabilité est une des bases de l’apprentissage non supervisé. Elle consiste à caractériser un ensemble de données en essayant de déterminer la loi de probabilité qui l’aurait généré : chaque point de données est vu comme une réalisation aléatoire de l’évènement suivant la dite loi de probabilité.
Par exemple, reprenons nos images de chats (sans nous préoccuper des chiens). Qu’est-ce qui caractérise une image de chat ? À partir de notre ensemble d’images d’entrainement, on peut essayer de déterminer la loi de probabilité sur tous les pixels d’une image qui représente un chat. Étant donné la couleur du pelage, on peut par exemple s’attendre à avoir beaucoup de pixels de cette couleur. La photo aura aussi sûrement un ou deux disques clairs pour les yeux. En revanche, il est moins probable qu’une image de chat comporte un motif de pois violets sur un fond jaune fluo. La loi de probabilité qui génère les images de chat reflète ces observations basiques, mais elle incorpore également des informations bien plus complexes, qu’on ne saurait énumérer et qui font d’un chat un chat. C’est la force de l’apprentissage automatique de pouvoir extraire ces informations de l’ensemble des données d’entrainement.
En pratique, pour cet apprentissage non supervisé, l’algorithme n’apprend plus une fonction paramétréea qui associe une sortie à une entrée, mais une loi de probabilité paramétrée. Comme précédemment, la valeur des paramètres est ajustée en fonction des données d’entrainement.
Prenons un nouvel exemple concret. Admettons que l’on veuille modéliser la loi de probabilité qui caractérise un jet de pièce. Nous avons deux réalisations (ou états) possibles, « pile » ou « face ». Pour formaliser notre problème, nous utiliserons un premier paramètre \(p_1\) pour la probabilité de pile (\(\mathbb{Prob}(\text{« pile »})=p_1\)), et un second paramètre \(p_2\) pour la probabilité de face (\(\mathbb{Prob}(\text{« face »})=p_2\)). Quelle valeur leur attribuer ? Remarquons pour commencer que les paramètres sont ici directement des probabilités, ce qui impose d’une part que \(p_1\) et \(p_2\) soient entre 0 et 1 et d’autre part que \(p_2+p_1=1\). Cette deuxième équation s’appelle contrainte de normalisation : la somme des probabilités sur l’ensemble des états possibles est égale à 1b.
Outre ces considérations mathématiques, nous avons accès à un ensemble de données d’entraînement, sous la forme du résultat de jets de pièce indépendants (« face », « pile », « pile », « face », « pile » etc …). Un algorithme intuitif d’apprentissage consiste à compter le nombre d’apparition de « pile » versus le nombre d’apparition de « face » dans la séquence d’entraînement puis de diviser ces comptes par le nombre total de jets pour fixer les valeurs des paramètres \(p_1\) et \(p_2\). Si la pièce n’est pas biaisée à peu près la moitié des jets d’entraînement seront « pile » et le reste « face », et les valeurs de \(p_1\) et \(p_2\) que nous en déduirons seront proches de 0,5.
À la fin des opérations, on peut créer de nouvelles données à partir de la loi de probabilité définie par les valeurs finales, dites entraînées, de \(p_1\) et \(p_2\). Pour générer un nouveau point de donnée, on décide avec une probabilité \(p_1\) que le résultat est « pile », sinon le résultat est « face ». On dit que la loi de probabilité apprise est un modèle génératif de nos données d’entraînement. Sur l’exemple des images de chats, le modèle résultant de l’apprentissage devrait permettre de générer de nouvelles images de chat. Pour fixer les idées, la figure 1 schématise la différence entre algorithme de classification et algorithme génératif sur nos exemples de chats.
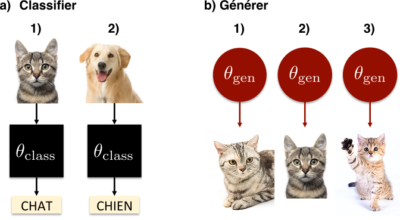
Néanmoins, les données sous forme d’images sont beaucoup plus complexes que le résultat d’un simple jet de pièce. Par conséquent, elles nécessitent des modèles de loi de probabilité bien plus sophistiqués. Celui que nous allons examiner appartient aux fondements de la physique.
Quand la physique s’en mêle : la loi de Boltzmann
En physique, un système à l’équilibre en contact avec un thermostat est caractérisé par la loi de Boltzmann. C’est-à-dire, la probabilité qu’a le système d’être dans un état donné est
$$\mathbb{Prob}(\text{état}) = \frac{e^{-E(\text{état})/k_B T }}{Z} \, ,$$
où \(E\) est la fonction d’énergiec, \(T\) la température et \(k_B\) la constante de Boltzmann. \(Z\), appelée fonction de partition, est déterminée par la contrainte de normalisation : la somme des probabilités sur l’ensemble des états possibles du système doit être égale à 1. En français, cette loi nous dit qu’à une température fixée plus l’énergie d’un état est faible plus il est probable (jetez un œil à la figure 2). Il est possible de vérifier par des expériences en laboratoire la validité de cette loi physique qui gouverne le monde. Nous allons voir dans la suite qu’elle peut aussi être pertinente au-delà de la description de la nature.
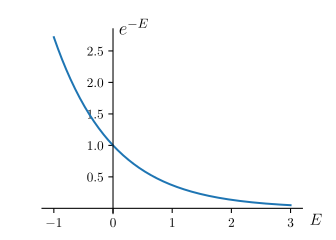
Les machines de Boltzmann
En apprentissage non supervisé, on peut se servir de la loi de Boltzmann pour définir une loi de probabilité paramétrée. Pour cela on commence par choisir une fonction paramétrée qui associe une « énergie » à chaque point dans l’espace des données. Pour fixer les idées, on peut utiliser la notation \(E_\theta(\mathrm{point\, de\, donnée})\) où \(\theta\) symbolise l’ensemble des paramètres de la fonctiond. Cette fonction « énergie » est ensuite insérée dans la définition de loi de Boltzmann pour définir une loi de probabilité
$$\mathbb{Prob}(\text{point de donnée}) = \frac{e^{-E_\theta(\text{point de donnée})/k_B T}}{Z}$$
appelée dans ce contexte machine de Boltzmann.
Notez que l’énergie \(E_\theta\) dont il est question, ici, n’a rien de physique. On a toute liberté pour la choisir afin de décrire les propriétés statistiques des données. Ses paramètres \(\theta\) sont ajustés pendant l’entraînement de manière à minimiser l’énergie des points de données d’entraînement, et donc à en maximiser la probabilitée.
Reprenons notre exemple d’apprentissage non supervisé sur des photos de chat. À partir d’une base de données d’images de \(500 \times 500\) pixels, nous souhaitons générer de nouvelles images de chats. Un point dans l’espace de nos données correspond à une image arbitraire de \(500 \times 500\) pixels. Elle peut représenter la Joconde, ou un chat, ou une juxtaposition aléatoire de couleurs. Notre objectif est de trouver les paramètres \(\theta\) de la fonction énergie \(E_\theta\) d’une loi de Boltzmann, qui attribuent une haute probabilité (une faible énergie) uniquement aux images de chats. Pour ce faire, nous présentons à l’algorithme la base de données d’entraînement d’images de chats et les valeurs des paramètres sont ajustées (ou apprise) en fonction. Si l’algorithme d’entrainement est capable de trouver des bonnes valeurs de \(\theta\), notre machine de Boltzmann attribuera une grande probabilité à n’importe quelle image de chat, même à celles qu’elle n’a jamais vu pendant l’entrainement. L’entrainement est alors réussi et on peut se servir à volonté de la machine de Boltzmann pour générer des images de chat !
Le problème de la fonction de normalisation
Mais, voilà, il y a un hic. Dans le paragraphe précédent, nous avons omis d’expliquer comment s’effectue l’optimisation des paramètres de la loi de Boltzmann au cours de l’entrainement. C’est une tâche qui se révèle hautement délicate. Sans entrer dans tous les détails mathématiques de cette optimisation, on peut facilement identifier la difficulté majeure. Il n’est pas possible de calculer exactement la probabilité que notre modèle attribue à une image donnée. Comment ça ?
Rappelons que la probabilité attribuée par notre machine de Boltzmann à une image est
$$\mathbb{Prob}(\text{image}) = \frac{e^{-E_\theta(\text{image})/k_BT}}{Z}$$
et que \(Z\) garantit la normalisation. Un calcul simple permet de voir que $Z$ est donc égale à la somme sur toutes les images possibles du terme \(e^{-E_\theta(\text{image})/k_BT}\). Facile ? Eh bien non, il est tout à fait impossible d’effectuer cette somme car elle contient un nombre de termes absolument gigantesque. Même en simplifiant notre problème avec des pixels qui pourraient uniquement être noirs ou blancs, il y aurait déjà \((\text{nombre d’état possible d’un pixel}) ^{\text{(nombre de pixels)}} = 2^{(500 \times 500)}\) différentes images possibles. Même les ordinateurs les plus puissants, sont incapables d’additionner un à un autant de termes en un temps raisonnable. Calculer \(Z\), et a fortiori \(\mathbb{Prob}(\text{image})\), est donc impossible !
C’est le problème du calcul de la fonction de partition \(Z\) auquel les physiciens se heurtent depuis la naissance de ces théories. Pour y remédier, ils ont imaginé, et continuent d’imaginer, différentes techniques d’approximation. Ces méthodes à la pointe des connaissances en physique peuvent donc être utiles à l’apprentissage automatique et c’est ce que nous avons étudié.
De la physique pour générer des images
Dans l’article que nous avons récemment présenté à la conférence NIPS (2015) [1], nous utilisons une technique d’approximation provenant de la physique pour proposer un nouvel algorithme d’entrainement des machines de Boltzmann. Cette approximation, dite de TAPf, nous sert à évaluer la valeur de la fonction de partition \(Z\) et à lever ainsi la difficulté principale de l’entrainement. Une application minutieuse de cette approximation nous a permis de mettre au point un nouvel algorithme d’entrainement.
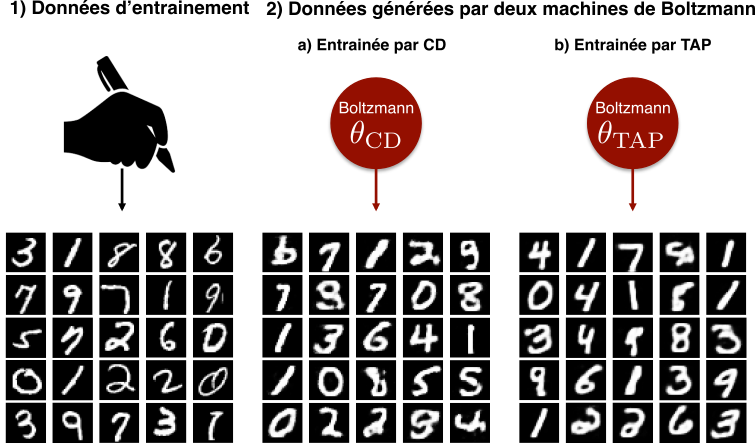
Nous avons choisi d’essayer notre stratégie sur une base de données qui contient des images de chiffres manuscrits (un peu plus faciles que des chats). C’est une base de référence en apprentissage automatique pour valider un algorithme. Le test que nous présentons ici consiste à comparer les images générées par une machine de Boltzmann entrainée avec le nouvel algorithme, aux images d’entrainement (regardez la figure 3 et sa légende !). Le résultat n’est pas parfait mais notre machine de Boltzmann semble capable d’imaginer des chiffres manuscrits plutôt convaincants et, ce, en différentes versions. Comme vous pouvez aussi le voir sur la figure, les performances de notre stratégie sont similaires à celles d’un autre algorithme appelé Contrastive Divergence [3] (proposée par Hinton en 2001). Notre alternative est équivalente en terme de résultat. Cependant, ses avantages et ses inconvénients diffèrent de ceux du premier algorithme et suivant les usages, l’un ou l’autre, peut s’avérer mieux adapté.
Conclusion
Nous avons présenté ici une application d’apprentissage automatique qui tire avantage de résultats obtenus en physique théorique. Le dialogue entre les communautés scientifiques n’est pas toujours aisé mais c’est une source de collaborations remarquablement fructueuses. À l’avenir, il est probable que ce soit l’apprentissage automatique qui à son tour rende service à la physique. Ces nouveaux outils, qui arrivent aux mains des physiciens, constituent une véritable révolution dans le traitement des données. Ils permettront sans doute de nouvelles grandes découvertes.
Notes
| a. | ↑ | Une fonction paramétrée est une fonction dont la définition dépend d’une ou plusieurs variable(s) appelée(s) paramètre(s). Par exemple on peut définir la fonction \(f_a\), qui étant donné la valeur du paramètre réel \(a\) associe au nombre réel \(x\), \(f_a(x)=a + x\). De même on peut définir la fonction \(f_{a,b,c}\) qui associe au réel \(x\), étant donné la valeur des paramètres réels \(a\), \(b\) et \(c\), \(f_{a,b,c}(x) = \text{« chat »}\) si \(ax^2+bx+c > 0\) et la valeur « chien » si \(ax^2+bx+c \leq 0\). |
| b. | ↑ | Elle implique qu’un seul des deux paramètres est nécessaire car la valeur du second paramètre est directement donnée par la valeur du premier selon \(p_2 = 1 -p_1\). |
| c. | ↑ | En physique, on commence toujours par définir le système, c’est-à-dire à délimiter la portion de l’univers étudiée. On peut ensuite définir l’énergie \(E\) du système qui dépend de son état. Prenons l’exemple d’un système mécanique : une masse \(m\) ponctuelle dans le référentiel terrestre. L’état du système est défini par la position de la masse ponctuelle \(\vec{r} = (x,y,z)\in \mathbb{R}^3\), et sa vitesse \(\vec{v} \in \mathbb{R}^3\). Son énergie est la somme de son énergie cinétique \(E_c=m\Vert \vec{v} \Vert^2/2\) et de son énergie potentielle de pesanteur \(E_{pp}=mgz\) (en prenant comme origine des potentiels \(z=0\)). Soit finalement une fonction énergie de l’état du système donnée par \(E(\vec{r},\vec{v}) = m\Vert \vec{v} \Vert^2/2 + mgz\). L’énergie d’un état augmente avec sa vitesse et sa position suivant \(z\), soit son altitude. |
| d. | ↑ | dont nous n’avons pas ici spécifié la forme exacte |
| e. | ↑ | Souvenez-vous, plus l’énergie est faible, plus la probabilité est grande pour une loi de Boltzmann ! |
| f. | ↑ | du nom des trois physiciens qui l’ont introduite en 1977, Thouless Anderson et Palmer [2] |









