L’Antarctique, si loin mais si proche…
L’Antarctique fait rêver les aventurier.ères depuis des siècles. Sa couverture de glace (appelée calotte ou inlandsis) est épaisse de parfois plusieurs kilomètres et recouvre un continent de la taille du Canada et de l’Union européenne combinés. En plus, elle se situe à un endroit symbolique : à l’extrême Sud du globe terrestre. Par son climat inhospitalier, avec des températures glaciales et des tempêtes souvent violentes, l’Antarctique a résisté longtemps à l’« envahisseur » humain. Elle est donc restée une région peu peuplée (quelques stations scientifiques) et entourée d’un certain mystère. Et pourtant… ce qui s’y passe actuellement ne devrait pas nous laisser de glace…
Malgré son éloignement des principales activités humaines, la région est de plus en plus affectée par le changement climatique qui en résulte. Depuis la révolution industrielle dans la deuxième moitié du 19e siècle, nous émettons de plus en plus de gaz à effet de serre dans l’atmosphère, entraînant un réchauffement global. Or, nous le savons tous.tes : quand il fait chaud, la glace fond, et se transforme en eau liquide. Si d’énormes masses de glace fondent et se déversent dans l’océan, cela entraîne une hausse du niveau des mers ! Par exemple, si toute la glace posée sur le continent Antarctique fondait, cela représenterait une hausse du niveau des mers autour de 60 m, ce qui changerait le pourtour de tous les continents ! En conclusion : « Ce qui se passe chez nous, ne reste pas chez nous » et « Ce qui se passe en Antarctique, ne reste pas en Antarctique ».
Chaud devant (et en-dessous)
Pour l’instant, heureusement, le réchauffement global de l’atmosphère n’affecte que certaines régions de l’Antarctique, surtout autour de la péninsule (la partie un peu longue qui pointe vers l’Amérique du Sud). En fait, plus l’atmosphère se réchauffe, plus elle peut contenir de vapeur d’eau et peut donc aussi produire plus de chutes de neige sur le continent. Cela contrebalancerait (une partie de) la fonte. Cependant, avec le réchauffement global, ce n’est pas seulement l’atmosphère qui se réchauffe. Non, l’océan, lui aussi, se réchauffe. Et c’est là que commence une chaîne de problèmes…
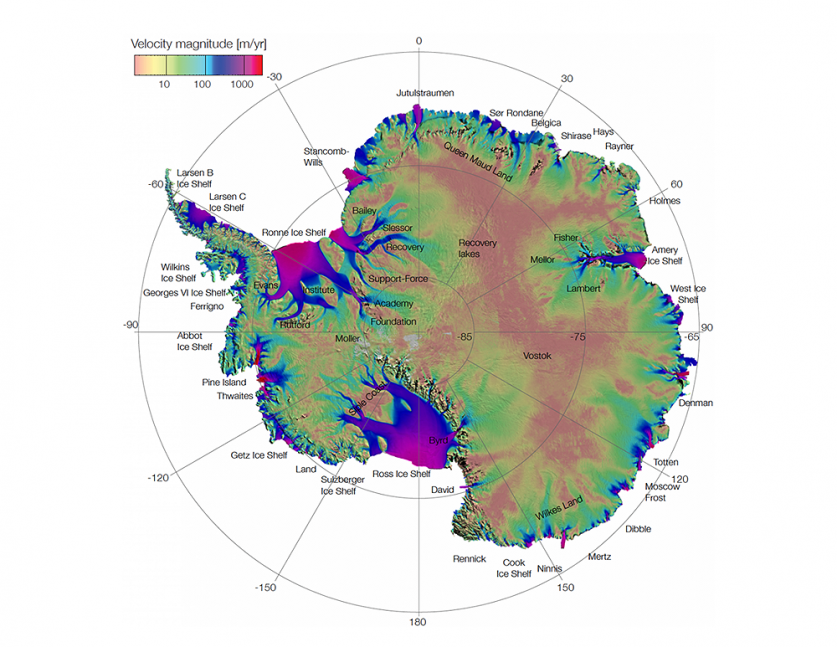
La calotte est le résultat de millions d’années de précipitations neigeuses sur le continent Antarctique. Au fur et à mesure du temps, les couches de neige plus récentes ont mis de plus en plus de pression sur les couches de neige plus anciennes, les transformant progressivement en glace. Sous ce poids grandissant et sur un relief rocheux qui n’est pas plat, la glace coule du centre du continent vers l’extérieur, sous l’effet de la gravité [voir la Figure 1 ou cette vidéo] comme une rivière, mais beaucoup plus lentement, puisque la glace est un matériau plus visqueux que l’eau. À la fin de leur chemin, ces « rivières de glace » atteignent l’océan, et forment des plateformes flottantes (ice shelfs pour les intimes) qui avancent sur l’océan jusqu’à se détacher morceau par morceau sous forme d’icebergs qui dérivent dans l’océan jusqu’à y fondre complètement.
Les plateformes flottantes agissent comme des freins sur la vitesse d’écoulement de ces « rivières », surtout lorsque les plateformes sont contraintes sur les côtés ou en dessous par des reliefs rocheux. De cette façon, elles ralentissent le flux de glace de la partie posée vers la partie flottante, sachant que c’est ce flux qui va déterminer la contribution de la calotte à la montée du niveau des mers. Les plateformes modèrent donc à quelle vitesse le niveau des mers monte. Or, l’océan, nous disions, se réchauffe…
Simuler les interactions entre l’océan et la glace – pourquoi et comment ?
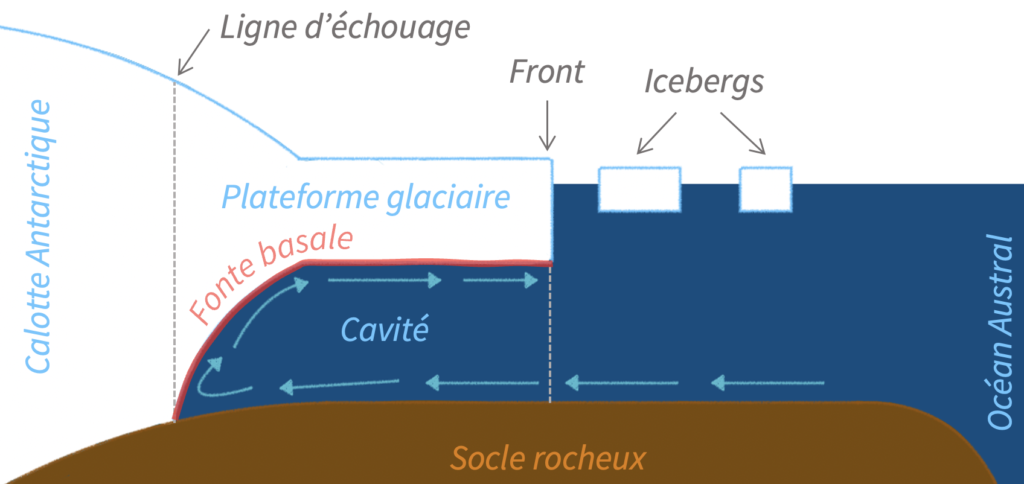
En conséquence du réchauffement océanique, des eaux plus chaudes entrent en contact avec la base des plateformes flottantes. Au contact de l’eau chaude, la fonte basale des plateformes augmente, ce qui les amincit, fait reculer leur front (la ligne délimitant la glace et l’océan non recouvert de glace) et fait reculer leur ligne d’échouage (la ligne délimitant la partie flottante et la partie posée de la glace) vers l’intérieur du continent [voir Figure 2]. Étant ainsi moins stables, elles ne peuvent plus freiner aussi efficacement le flux de glace vers l’océan.
Pour simuler l’effet de la fonte actuelle et faire des projections de l’effet futur des plateformes glaciaires sur le flux de glace du continent vers l’océan (et donc sur la hausse du niveau des mers !), nous utilisons des modèles physiques décrivant l’évolution de la calotte. Pour guider les simulations de ces modèles, il faut des informations sur la fonte par l’océan à la base des plateformes, car les modèles de calotte ne simulent pas la circulation océanique.
La fonte basale est un processus qui a lieu lorsque l’océan en contact avec la glace est plus chaud que la température de fusion locale. La différence entre la température de l’eau et la température de fusion est appelée forçage thermique. La température de fusion de l’eau dépend de sa salinité et de la pression locale. Nous le savons toutes et tous : pour de l’eau douce à pression ambiante, cette température de fusion est de 0°C. Par contre, l’océan contient du sel et l’interface océan-glace se trouve à plusieurs centaines de mètres sous la surface, donc à pression élevée. En conséquence, pour calculer la chaleur disponible pour la fonte, il faut prendre en compte la température de l’océan, la salinité de l’océan et la profondeur de la glace (qui est directement reliée à la pression).
En plus de la différence directe de température entre l’océan et la glace, de la chaleur additionnelle peut être ajoutée par de la turbulence créée lorsque de l’eau de fonte formée près de la ligne d’échouage monte le long de la base de l’ice shelf. Cette eau de fonte, ayant une salinité moins haute que l’océan ambiant, est moins dense que celui-ci. Plus la différence de densité est haute, plus rapide sera le courant qui déplacera cette eau et plus grande sera la probabilité d’avoir des turbulences à l’interface océan-glace. Ces turbulences peuvent entraîner sur leur chemin des eaux potentiellement plus chaudes qui, au départ, ne se trouvaient pas directement en contact avec la glace. En conséquence, (une partie de) ces eaux chaudes peuvent se retrouver en contact avec la glace.
En résumé, donc, pour calculer la fonte basale, nous avons besoin des propriétés de l’océan tout au long de l’interface océan-glace. Et ces propriétés dépendent de la température et salinité de l’océan devant la plateforme mais aussi de la circulation dans la cavité sous la plateforme.
Mais, voilà, ce n’est pas si facile de comprendre la circulation océanique et les échanges océan-glace dans cette cavité car elle est très difficilement observable. Les satellites ne « voient » pas sous la couverture de glace et les bateaux ne peuvent pas y accéder non plus. Depuis quelques années, nous commençons à avoir des données par de nouvelles méthodes : les véhicules sous-marins téléopérés (Remotely Operated Vehicles, ROV) et les capteurs fixés sur des mammifères marins, principalement des éléphants de mer (MEOP). Mais, ces méthodes ne donnent pour l’instant que des observations limitées dans l’espace et dans le temps…
Que choisir ? – Édition « Paramétrisations de fonte basale »
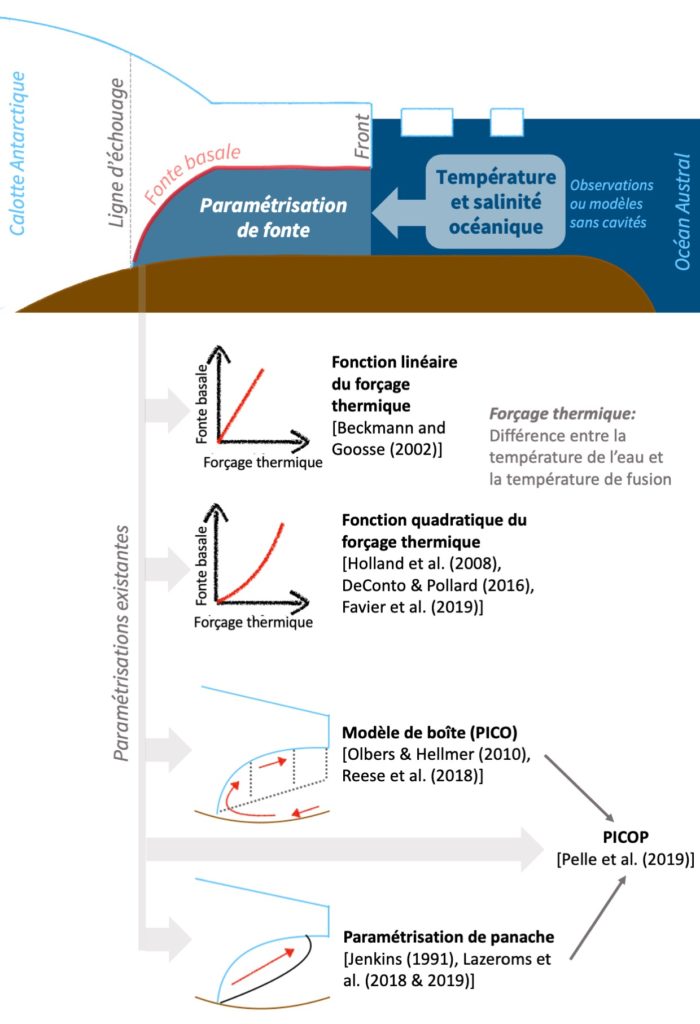
Au cours des dernières décennies, plusieurs formulations simplifiées (paramétrisations pour les intimes) ont été développées pour décrire le lien entre la température et la salinité de l’océan devant une cavité (telles que données par des observations ou des simulations d’océan global qui ne prennent pas en compte les cavités de plateformes glaciaires) et la fonte à la base de la plateforme glaciaire [voir Figure 3]:
- Les paramétrisations dites “simples” supposent que la fonte basale est une fonction linéaire [Beckmann & Goosse, 20021] ou quadratique [Holland et al. 20082, De Conto & Pollard 20163, Favier et al. 20194] de la différence entre la température de l’eau et la température de fusion locale.
- Le modèle de boîte découpe la circulation circulaire dans la cavité en différentes boîtes et calcule les propriétés de l’eau dans chaque boîte au fil du mouvement du courant d’eau de fonte [Olbers & Hellmers 20105, Reese et al. 20186].
- La paramétrisation de panache inclut la formation d’un panache d’eau de fonte au niveau de la ligne d’échouage qui s’élève le long de la base de la plateforme et inclut donc l’effet de la turbulence sur la fonte [Jenkins 19917, Lazeroms et al. 20188 & 20199].
- PICOP utilise le modèle de boîte pour calculer la température et salinité au fil du mouvement et utilise la paramétrisation de panache pour inclure l’effet du panache de fonte [Pelle et al. 201910].
Toutes ces paramétrisations contiennent un ou deux paramètres libres qui sont généralement ajustés en comparant les résultats des paramétrisations avec des observations ou, s’il n’y a pas d’observation, une autre sorte de référence. Dans le passé, ces formulations ont été ajustées pour reproduire le comportement de fonte d’un nombre limité de plateformes glaciaires pour lesquelles il y a les deux informations nécessaires : des observations des propriétés océaniques devant la cavité et des estimations de fonte basale. Malheureusement, quand elles ont été appliquées ainsi sur d’autres plateformes, les résultats ne correspondaient pas toujours bien aux estimations de fonte de celles-ci.
C’est dans ce contexte que nous avons commencé notre étude [Burgard et al. 2022]11. Nous ? C’est moi, postdoc novice dans le domaine des plateformes glaciaires à l’époque, Nicolas Jourdain, expert entre autre des paramétrisations quadratiques, Pierre Mathiot, expert de simulations océaniques globales et des cavités sous les plateformes glaciaires, Ronja Reese, développeuse de la version la plus récente du modèle de boîte, et Adrian Jenkins, développeur de la paramétrisation de panache. En ayant des expert.e.s de la plupart des variantes de paramétrisations à bord, nous voulions montrer que l’étude n’avait pas vocation à être biaisée vers une paramétrisation particulière.
Notre étude est basée sur une idée présentée dans une étude précédente réalisée par Favier et al. en 20194. Il s’agit d’utiliser une “réalité virtuelle” pour ajuster les paramètres libres. Favier et al. (2019) l’avaient fait avec une seule plateforme à géométrie idéalisée. Nous sommes allés plus loin pour ajuster les paramètres libres sur un plus grand nombre de plateformes glaciaires (35 pour être précise), distribuées sur tout le pourtour de l’Antarctique. Pour cela, nous avons utilisé des simulations produites par un modèle d’océan global en les considérant comme une “réalité virtuelle”. Ce modèle simule la circulation océanique tout autour du globe et, dans cette configuration particulière, aussi la circulation dans les cavités sous les plateformes et même la fonte basale qui en résulte.
Petite parenthèse ici: vous vous demandez peut-être pourquoi on a besoin de paramétrisations si on a des modèles d’océans qui peuvent simuler la circulation dans les cavités ? Eh bien, ces modèles d’océan sont très coûteux en termes de calcul et ne sont donc pas (encore) adaptés pour des simulations sur plusieurs centaines d’années, nécessaires pour les projections d’élévation du niveau des mers, ou pour des ensembles de simulations, nécessaires pour estimer les incertitudes dans les différents degrés de liberté.
Revenons à nos paramétrisations. Notre réalité virtuelle nous fournit un parfait bac à sable pour ajuster les paramètres libres. Elle nous apporte toutes les informations dont nous avons besoin : la température et la salinité devant les différentes cavités, et les fontes basales résultantes. Dans ce contexte, nous avons ajusté les paramètres libres pour reproduire du mieux possible la fonte basale de notre réalité virtuelle avec les différentes paramétrisations.
Dans un second temps, nous avons comparé les fontes basales résultantes des différentes paramétrisations pour donner des recommandations pour l’utilisation dans les modèles de calotte. Dans la figure 4, vous pouvez voir un exemple de fonte basale pour trois plateformes glaciaires “connues”: les plateformes de Filchner-Ronne et Ross, les deux plus grandes de l’Antarctique, et la plateforme du Pine Island Glacier, qui se trouve dans la mer d’Amundsen, la région où les plateformes de glace sont en train de fondre très rapidement en ce moment en conséquence d’eaux assez chaudes qui atteignent leur base [voir figure 1 pour leur localisation]. Sur cet exemple, vous pouvez voir qu’aucune paramétrisation ne fait un job “parfait”. En plus, il n’y a pas une paramétrisation unique qui s’avère meilleure pour toutes les plateformes, cela dépend plutôt de la plateforme que l’on étudie. Dans cette figure, nous présentons différentes variations de la paramétrisation quadratique et de la paramétrisation de panache que je ne vais pas expliquer plus en détail ici mais vous pouvez voir que, pour une même paramétrisation de base, les variations peuvent donner des résultats assez différents (pour rendre les choses simples…).
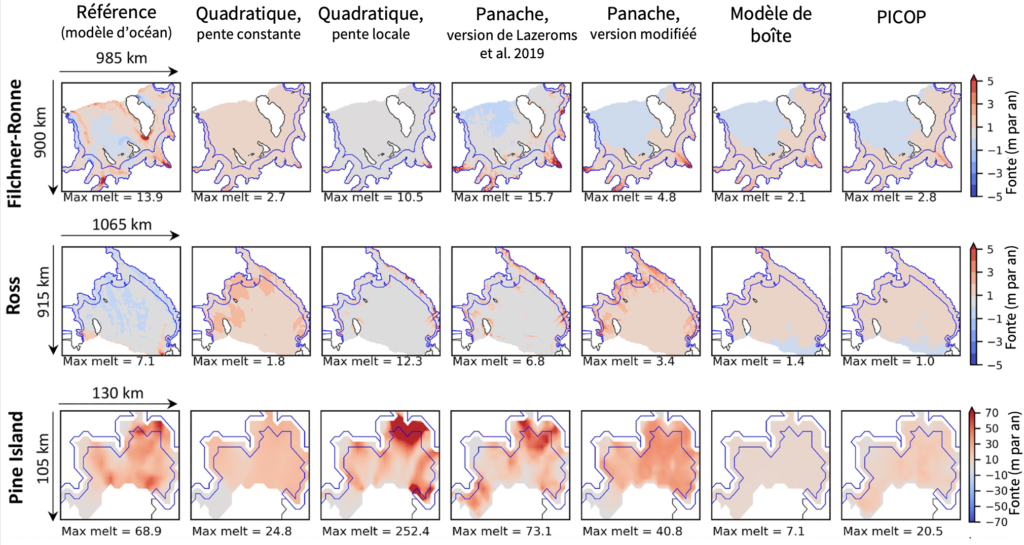
Par exemple, la 2e et 3e colonne utilisent une paramétrisation quadratique mais définissent la pente de la glace différemment. Vous voyez que, pour Filchner-Ronne, la quadratique à pente constante donne une fonte autour de 2 m par an à peu près partout alors que la quadratique à pente locale donne une fonte sous 1 m par an sur la plupart du domaine mais présente une fonte très haute à certains endroits près de la ligne d’échouage allant jusqu’à 10,5 m par an. Pour Pine Island c’est encore plus extrême. La fonte maximale est autour de 25 m par an pour la première (bien en dessous des 69 m par an de notre référence) alors que, pour la deuxième, la fonte maximale atteint 252 m par an (bien au-dessus de notre référence…).
Afin de pouvoir faire des recommandations, nous avons mesuré la différence entre les prévisions de fonte annuelle résultant des paramétrisations et celles de notre réalité virtuelle. Pour chacune des plateformes, nous avons fait ce calcul une première fois en prenant en compte toute la plateforme puis seulement concernant la zone près de la ligne d’échouage (délimitée en bleu dans la figure 4). C’est en identifiant les valeurs les plus basses pour les deux métriques, que nous avons pu faire des recommandations. Nos résultats suggèrent que la paramétrisation quadratique et la paramétrisation de panache donnent les meilleurs résultats. Ce résultat est plutôt surprenant puisque la paramétrisation quadratique est vraiment très simpliste et nous aurions plutôt attendu que le modèle de boîte et la paramétrisation de panache ressortent clairs “vainqueurs” de cette comparaison.
Un autre message important ressortant de cette étude est que toutes les paramétrisations restent très incertaines et qu’elles restent toutes probablement trop simples pour décrire la variété des processus qui affectent la fonte basale des plateformes glaciaires. Il reste donc encore beaucoup de travail pour mieux quantifier et réduire ces incertitudes.
Un regard vers le futur…
Heureusement, plusieurs projets européens (tels que PROTECT, TiPACCs, OCEAN:ICE) se penchent actuellement sur les incertitudes des simulations futures de l’Antarctique pour mieux comprendre et estimer la hausse du niveau marin qui nous attend dans les prochaines décennies, siècles et millénaires. En même temps, la pression pour atteindre rapidement ces objectifs monte chaque jour. Rappelons-nous que le réchauffement global s’accélère et que les émissions de CO2 ne sont pas vraiment en train de diminuer…
Pour aller plus loin…
European Geosciences Union Image of the Week — Where do people stay in the « coolest » place on Earth?
Wikipedia: Élevation du niveau de la mer
Marine Ice Sheet Instability « For Dummies »
European Geosciences Union Image of the Week — ROVing in the deep…
Marine Mammals Exploring the Oceans Pole to Pole
Bibliographie
- 1 A. Beckmann, and H. Goosse, “A parameterization of ice shelf–ocean interaction for climate models,” Ocean Modelling, 157–170 (2003).
- 2 P.R. Holland, A. Jenkins, and D.M. Holland, “The Response of Ice Shelf Basal Melting to Variations in Ocean Temperature,” Journal of Climate, 2558–2572 (2008).
- 3 R.M. DeConto, and D. Pollard, “Contribution of Antarctica to past and future sea-level rise,” Nature, 591–597 (2016).
- 4 L. Favier, N.C. Jourdain, A. Jenkins, N. Merino, G. Durand, O. Gagliardini, F. Gillet-Chaulet, and P. Mathiot, “Assessment of sub-shelf melting parameterisations using the ocean–ice-sheet coupled model NEMO(v3.6)–Elmer/Ice(v8.3),” Geosci. Model Dev., 2255–2283 (2019).
- 5 D. Olbers, and H. Hellmer, “A box model of circulation and melting in ice shelf caverns,” Ocean Dynamics, 141–153 (2009).
- 6 R. Reese, T. Albrecht, M. Mengel, X. Asay-Davis, and R. Winkelmann, “Antarctic sub-shelf melt rates via PICO,” The Cryosphere, 1969–1985 (2018).
- 7 A. Jenkins, “A one‐dimensional model of ice shelf‐ocean interaction,” J. Geophys. Res., 20671–20677 (1991).
- 8 W.M.J. Lazeroms, A. Jenkins, G.H. Gudmundsson, and R.S.W. van de Wal, “Modelling present-day basal melt rates for Antarctic ice shelves using a parametrization of buoyant meltwater plumes,” The Cryosphere, 49–70 (2018).
- 9 W.M.J. Lazeroms, A. Jenkins, S.W. Rienstra, and R.S.W. van de Wal, “An Analytical Derivation of Ice-Shelf Basal Melt Based on the Dynamics of Meltwater Plumes,” Journal of Physical Oceanography, 917–939 (2019).
- 10 T. Pelle, M. Morlighem, and J.H. Bondzio, “Brief communication: PICOP, a new ocean melt parameterization under ice shelves combining PICO and a plume model,” The Cryosphere, 1043–1049 (2019).
- 11 C. Burgard, N.C. Jourdain, R. Reese, A. Jenkins, and P. Mathiot, “An assessment of basal melt parameterisations for Antarctic ice shelves,” The Cryosphere, 4931–4975 (2022).









