Étudier les villes avec… de la physique !

Pour étudier l’évolution de la population des villes, je fais appel à l’économie et à la physique. En sciences, la pluridisciplinarité ne choque personne ! La physique ne se passe pas des mathématiques, la biologie de la chimie et histoire et géographie sont si inconsciemment liées que leur enseignement commun jusqu’au lycée paraît une évidence. Les croisements entre sciences naturelles et sociales paraissent quant à eux souvent plus excentriques. Ces originalités proviennent d’ailleurs le plus souvent d’excursions des sciences naturelles vers les sciences sociales (avec un succès plus ou moins limité) comme celles que les physiciens tentent depuis maintenant une trentaine d’années en économie.

Il faut reconnaître que l’utilisation extensive des mathématiques par les deux disciplines fournit une justification certaine à l’expédition. C’est pourtant d’une intuition théorique plus profonde et plus fondamentale que partent mes recherches.

Cette intuition repose sur une observation. L’économie cherche à écrire des lois simples pour décrire les échanges entre les hommes dont le comportement individuel est complexe et en partie aléatoire de la même manière que la physique (macroscopique) a réussi à écrire des lois simples pour décrire le monde malgré le fait que les particules élémentaires aient un comportement complexe et en partie aléatoire. Bref, l’économie comme la physique – et en particulier la physique statistique – s’intéressent à ces phénomènes de changements d’échelles, comme du petit vers le grand, que Claude Lévi-Strauss illustre très bien dans le cas de l’existence des villes :

 Mais la vie urbaine offre un étrange contraste. Bien qu’elle représente la forme la plus complexe et la plus raffinée de la civilisation, par l’exceptionnelle concentration humaine qu’elle réalise sur un petit espace et par la durée de son cycle, elle précipite dans son creuset des attitudes inconscientes, chacune infinitésimale mais qui, en raison du nombre d’individus qui les manifestent au même titre et de la même manière, deviennent capables d’engendrer de grands effets.

Pour que notre démarche ne soit pas inféconde, il faut bien sûr lui donner un sens empirique, c’est-à-dire être capable de montrer que les méthodes de la physique peuvent se transposer à des questions économiques avec un certain succès explicatif et prédictif. À la manière de Lévi-Strauss, nous pouvons noter que, parmi les phénomènes économiques, l’étude des villes est un laboratoire propice à de telles expérimentations. Les villes^​*​, aussi différentes soient-elles, se caractérisent par leurs similitudes qui se retrouvent dans toutes les cultures et à toutes les époques : des marchés, des lieux de pouvoir, un réseau de rues ou de transports, etc. Il paraît donc plausible de penser que les villes ont en commun des caractéristiques fondamentales qui justifient de pouvoir les étudier comme un concept unique de « la ville » dont on cherche à trouver les lois.

La question urbaine la plus naturelle pour l’économiste ou le physicien est alors celle de la population. Au premier ordre, la population est le facteur explicatif principal de ce qui a lieu dans une ville. Plus une ville est grande (au sens de sa population), plus elle est en valeur absolue riche, étendue, polluante, etc. Bien sûr, la valeur absolue n’a pas beaucoup d’intérêt. Il serait plus utile de savoir si, en se développant, une ville devient relativement plus riche, étendue, polluante, c’est-à-dire de connaître l’effet de la population dans les villes au second ordre. Malheureusement, on sait rarement conclure à un effet sous-linéaire ou super-linéaire – un économiste dirait à des rendements croissants ou décroissants – de la population sur d’autres caractéristiques urbaines, voir figure 1.

Mais quelle est la taille « typique » d’une ville ? L’économie est mal à l’aise pour répondre à cette question. Comme le rappelle Paul Krugman dans un célèbre article, « The mystery of urban hierarchy » , l’économie prédit que les villes sont à l’équilibre et qu’elles devraient donc être proches d’une taille optimale, équilibre entre optimisation des coûts de transport et synergies urbaines. Ce n’est pas le cas en pratique. Pis, il est établi depuis Auerbach que les tailles de villes sont distribuées de façon très inégalitaire selon une loi de puissance, la loi de Zipf : non seulement les villes ne font pas la même taille mais il n’existe même pas de taille typique des villes. Comme le déplore Krugman, ce sont alors des modèles mathématiques élémentaires « sans fondement économique » qui sont le plus capables de reproduire la réalité, comme si les détails de petite échelle n’importaient pas dans la construction urbaine, à la manière de ce que connaît la physique statistique.

Durant ma thèse , j’ai cherché à comprendre s’il était possible d’aller plus loin que ce constat un peu décevant, de trouver une raison plus « matérielle » à l’apparition de la loi de Zipf dans la distribution des populations de villes (Figure 2). Assez instinctivement, je me suis tourné vers les migrations interurbaines, une piste qui avait déjà été explorée par quelques économistes .

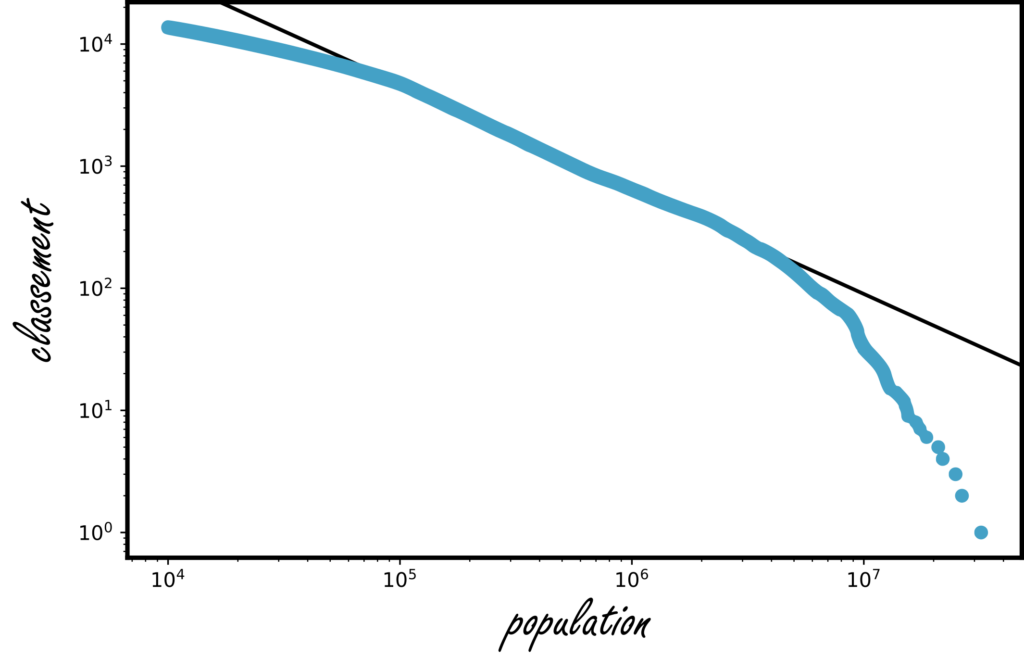
Ces migrations d’une ville à une autre sont empiriquement assez stables d’une année sur l’autre mais peuvent être, parfois, considérables. En fait, il arrive que la taille des arrivées (ou des départs) de population d’une ville en une année soit de l’ordre de la taille de la ville elle-même. Mathématiquement, nous observons que la distribution des flux migratoires interurbains est « à queue lourde » (long tail data). En sommant les flux sortants ou entrants totaux d’une ville, on note alors que ces flux sont distribués selon une « loi de Lévy », une forme plus générale et plus complexe de la loi normale, qui était jusqu’ici au cœur du modèle référence de la croissance urbaine .

Quantitativement, il est donc possible de réécrire les modèles de croissance urbaine de référence en remplaçant la loi normale par une loi plus compliquée, une loi de Lévy. Théoriquement, la loi de Lévy se caractérise par une probabilité plus importante d’observer des événements extrêmes, des chocs brutaux de populations. Avec mon directeur de thèse, Marc Barthélémy, nous avons montré que le modèle de Lévy est le plus indiqué pour expliquer comment certaines grandes villes peuvent disparaître en quelques années (ou d’autres émerger sur la même période). Par exemple, pendant la ruée vers l’or, la population de San Francisco passe d’un peu plus de 1000 à 150 000 habitants entre 1850 et 1870. Un tel changement ne peut pas avoir lieu dans un modèle de croissance à loi normale. Il est en revanche parfaitement compatible avec un modèle de Lévy.

Quel effet toutefois sur la distribution de la taille des villes ? Le modèle prédit une distribution proche de la loi de Zipf « à temps long » (1 000 – 10 000 ans) mais qui en diffère de façon importante à des échelles de temps réelles. En apparence, en contradiction avec le rôle central que la loi de Zipf joue en économie urbaine pour tester la validité d’un modèle, cette prédiction est en accord avec les données urbaines des vingt dernières années, qui remettent en cause la validité de la loi de Zipf en pratique . La loi de Zipf ne tient ni dans la plupart des pays, ni à la plupart des époques. Notre modèle le confirme et démontre même comment la loi de Zipf a pu être mesurée « par erreur » dans un grand nombre de cas comme beaucoup de lois de puissance. En effet, il est très facile d’observer la loi de Zipf sur un jeu de données si l’on effectue la mesure avec des méthodes statistiques simples, comme une régression linéaire . En faisant le test sur notre propre prédiction, pourtant assez différente de la loi de Zipf, nous avons remarqué qu’une mesure statistique classique prédisait un excellent accord ! En poussant le raisonnement, nous avons enfin montré que la mesure de la loi dépendait plus du nombre de villes choisies dans l’étude que d’autre chose, nous permettons d’affirmer que la loi de Zipf ne tient pas de façon générale (voir la Figure 3).

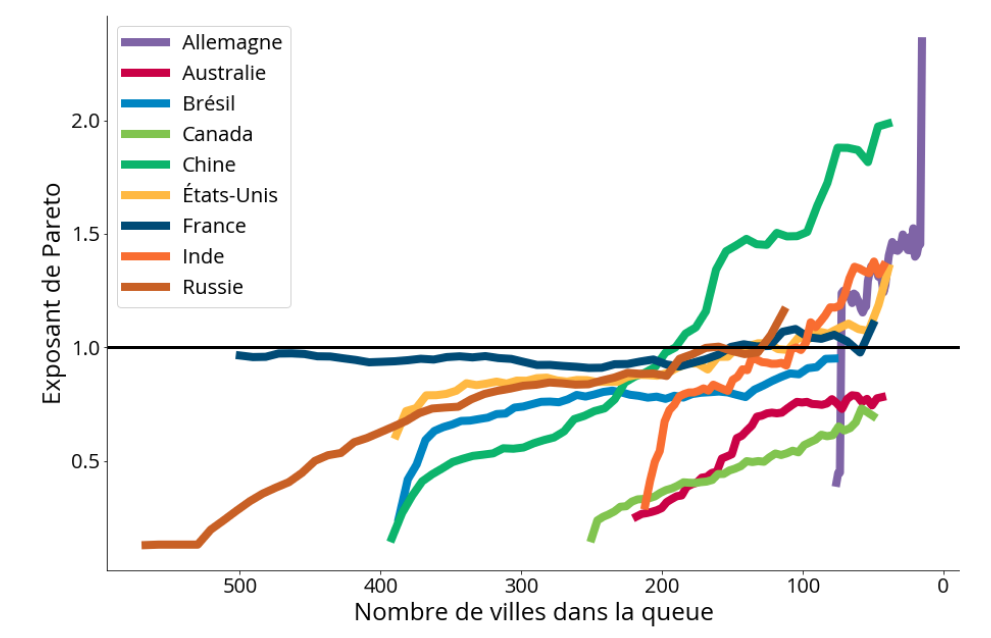
Plus précisément, dans chacun des pays, on choisit une taille de ville minimale \(S_\mathrm{min}\) et l’on mesure l’exposant (de Pareto) de la loi de puissance la plus proche de la distribution des tailles de villes plus grandes que \(S_\mathrm{min}\) correspondantes. Si la loi de Zipf était vérifiée, on s’attendrait à trouver une valeur constante (et proche de 1) pour chaque valeur de \(S_\mathrm{min}\). Or l’exposant trouvé est parfois très éloigné de la valeur attendue 1 et dépend fortement de \(S_\mathrm{min}\). Ce résultat souligne que la loi de Zipf n’est pas vraie en général puisque sa mesure dépend avant tout de la taille des villes considérées (selon un seuil arbitraire).

Ainsi, les récents résultats de nos recherches, présentés dans la revue Nature , apportent une perspective nouvelle sur le destin des villes. Le succès des villes dépend davantage de chocs extérieurs, qui peuvent éventuellement être provoqués et gérés, mais qui bouleversent le sort des villes en quelques années, que de l’accumulation lente d’effets aléatoires et inéluctables. De façon optimiste, c’est aussi une manière de dire que les décisions prises en matière de politique urbaine et d’aménagement du territoire jouent un rôle essentiel dans le renforcement de l’attractivité d’une ville et ont le pouvoir de modifier complètement sa trajectoire de développement et son histoire future.

Bibliographie