En juin 2016, après plus de trois ans de travail, les expériences que nous menons au Laboratoire Pierre Aigrain, en partenariat avec le Laboratoire Kastler Brossel ont conduit à la publication d’un article [1] dans la revue Physical Review Letters sur la manière de générer des photons uniques à partir de nanotubes de carbone. En effet, la génération de photons uniques – c’est à dire d’un flux de photons séparés les uns des autres par un temps non nul – est aujourd’hui un domaine de recherche à part entière, car c’est une étape essentielle pour la cryptographie quantique.
La cryptographie quantique est un moyen de sécuriser les échanges d’information, qui sont alors protégées d’un espionnage par les lois de la mécanique quantique (en particulier l’impossibilité de lire le message sans modifier le système, et le théorème de non-clonage qui stipule que copier des données quantiques est impossible). Cependant, la présence de plusieurs photons à la fois rend la cryptographie quantique vulnérable [2], d’où l’importance d’une source de photons uniques. Les nanotubes de carbone sont des candidats intéressants pour fabriquer un tel générateur car il est démontré qu’ils peuvent émettre des photons uniques à température ambiante et dans les bandes télécoms.
Cependant, les nanotubes présentent un défaut majeur : leur faible rendement radiatif. Considérons un système à deux niveaux d’énergie (fondamental et excité). Lorsqu’il est excité (par une impulsion électrique, un faisceau optique), un électron présent dans le niveau fondamental est promu dans le niveau excité. L’énergie acquise est alors relaxée par l’émission d’un photon dans une direction aléatoire de l’espace lorsque l’électron retombe dans son niveau fondamental. C’est ce qu’on appelle l’émission spontanée. On parle également de canal radiatif. Mais les nanotubes ne correspondent pas à ce système idéal : il existe un canal non-radiatif pour lequel la relaxation se fait sans émettre de photon (par exemple en relâchant l’énergie grâce à des vibrations). Ainsi lorsqu’un nanotube est excité, il a un taux d’émission de photon \(\gamma_R\) et il a un taux \(\gamma_{NR}\) de relaxation sans émission de photon, comme résumé sur la figure 1. Le taux de désexcitation total est donc \(\gamma=\gamma_R+\gamma_{NR}\) et le rendement radiatif est défini comme :
\(\eta = \frac{\gamma_R}{\gamma}=\frac{\gamma_R}{\gamma_R+\gamma_{NR}}\)
En général, il vaut 1%, ce qui est trop faible pour des applications industrielles.
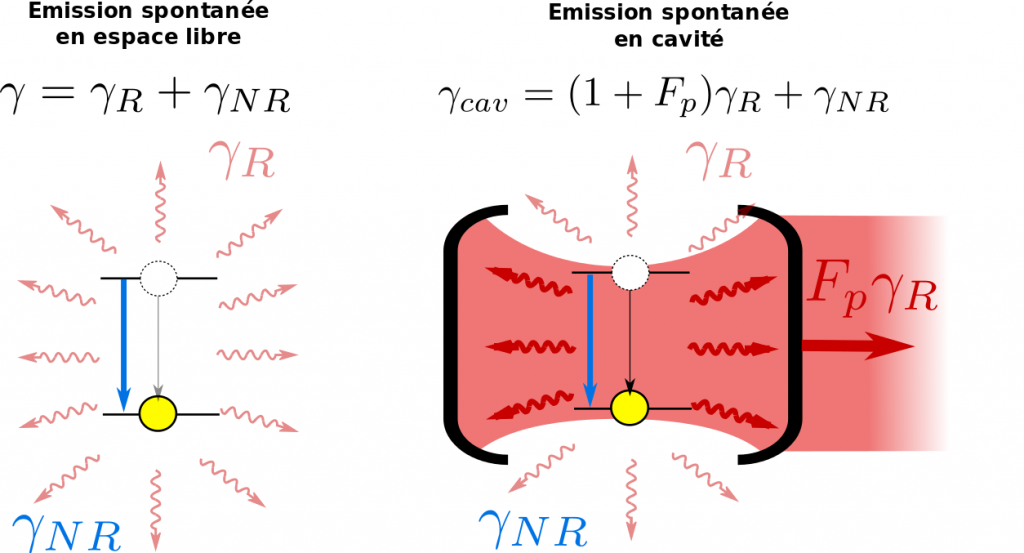
Dans nos article, nous montrons comment ce rendement radiatif peut être modifié grâce à la présence d’une cavité. Dans notre cas, il s’agit de deux miroirs se faisant face, en configuration dite de Fabry-Pérot. Les détails sont donnés dans cette vidéo. En effet, la présence d’une cavité modifie l’environnement électromagnétique du nanotube, et crée un nouveau canal de relaxation. Ce canal correspond à l’émission de photons dans le mode de la cavité, avec un taux \(F_p\gamma_R\). De plus, ce canal est directionnel, ce qui signifie que les photons émis peuvent facilement être récoltés (ici dans une fibre optique) pour être utilisés dans des applications.
\(F_p\), appelé facteur de Purcell, quantifie le taux d’émission spontanée dans le canal créé par la cavité. Autrement dit, le nouveau taux de désexcitation est donné par : \(\gamma_{cav}=(1+F_p)\gamma_R+\gamma_{NR}=\gamma(1+\eta F_p)\). Le rendement radiatif en cavité – défini comme le pourcentage de photons générés dans le mode cavité – devient alors :
\(\eta_{cav}=\frac{\eta F_p}{1+\eta F_p}\)
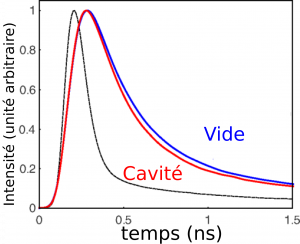
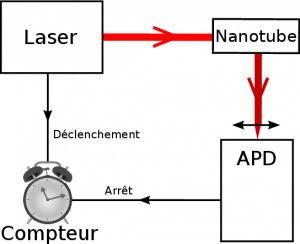
Pour mesurer ce phénomène, nous avons recours à un méthode temporelle, dont le résultat est affiché dans la figure 3 de notre article (remis ici en figure 2). Cette expérience consiste à mesurer et à comparer \(\gamma\) et \(\gamma_{cav}\). Le schéma de la figure 3 résume la façon dont cette mesure a lieu : un laser impulsionnel est utilisé pour exciter le nanotube. À chaque impulsion du laser, un compteur est déclenché. Cette impulsion excite le nanotube, qui relaxe. Si cette relaxation se fait par l’émission d’un photon, celui-ci est détecté par une photodiode à avalanche. Le compteur est alors arrêté et donne le délai entre l’excitation et l’émission d’un photon.
L’expérience est répétée des millions de fois en quelques minutes afin de construire un histogramme de ce délai. Cet histogramme ressemble en général à une exponentielle décroissante \(\exp(-\gamma t)\). L’expérience est réalisée deux fois : avec et sans la cavité de façon à obtenir \(\gamma\) et \(\gamma_{cav}\). Dans la figure 2, il est visible que l’obtention d’un photon est plus rapide avec la cavité plutôt que sans. Le facteur de Purcell, est obtenu par la formule \(F_p=\frac{1}{\eta}(\gamma_{cav}{\gamma}-1)\) et vaut 5. Autrement dit l’émission est 5 fois plus forte dans le mode de cavité qu’elle ne l’était sans la cavité. Depuis, nous avons obtenu des facteurs de Purcell dépassant 100, et des rendements en cavité proches de 50%.
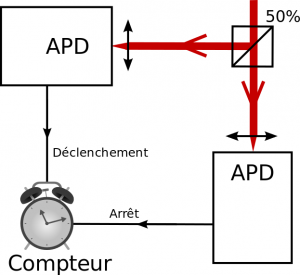
Après avoir démontré l’augmentation du rendement, nous nous sommes attachés à prouver que les photons émis par les nanotubes de carbone sont bien uniques. Pour cela, nous utilisons un dispositif dit de Hanbury-Brown et Twiss (HBT), schématisé dans la figure 4. Celui-ci consiste en un miroir semi-réfléchissant pour lequel les photons sont transmis ou réfléchis avec une chance sur deux. De chaque côté de ce miroir se trouve un détecteur. Lorsqu’un photon arrive sur le premier détecteur, un compteur est déclenché. Celui-ci s’arrête lorsqu’un autre photon atteint le second détecteur. Ainsi le compteur donne le délai entre la détection de deux photons. Comme pour l’expérience précédente, celle-ci est reproduite un grand nombre de fois afin de construire un histogramme.
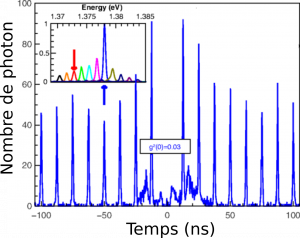
L’expérience est réalisée en excitation impulsionnelle, par conséquent l’histogramme ressemble à une série de pics (voir figure 5). En effet, le délai entre l’émission de deux photons est forcément un multiple du délai entre deux excitations : il faut attendre 0 excitation si deux photons sont émis puis détectés en même temps ; 1 excitation si un premier photon est envoyé sur un détecteur et celui de l’excitation suivante sur l’autre ; 2 excitations si deux photons d’affilé sont envoyés sur un détecteur et le troisième sur le second détecteur ; et ainsi de suite… Les valeurs négatives correspondent simplement à une permutation des détecteurs. Pour mieux se le représenter, le cas d’un délai égal à deux excitations est représenté dans la vidéo.
Le point crucial de cette expérience est que s’il n’y a jamais deux photons émis en même temps, il n’y a pas de possibilité de détecter deux photons en même temps et d’obtenir un délai nul. Par conséquent, l’absence d’un pic à délai nul est la preuve de l’émission de photons uniques.
Enfin, nous avons montré qu’une légère variation (de l’ordre du nanomètre) de la distance entre les miroirs de leur cavité provoque une variation dans la longueur d’onde d’émission du nanotube présent dans la cavité (voir encart supérieur gauche de la figure 5). Ceci est dû à la condition de résonance d’une cavité Fabry-Pérot : \(L =n\lambda/2\) où \(L\) est la longueur de la cavité, et \(\lambda\) la longueur d’onde d’émission. Nous montrons que la lumière générée conserve ses propriétés : un facteur de Purcell identique, et des photons uniques. Nous avons donc largement amélioré le rendement de notre source, tout en gardant une émission de photon uniques, ce qui était l’objectif pour des applications en cryptographie quantique. En plus, nous pouvons accorder cette source en longueur d’onde, ouvrant la voie au multiplexing, c’est à dire à la superposition de plusieurs messages à des longueurs d’ondes différentes dans une même fibre optique.













Good work…:-)