Lorsqu’une goutte d’eau est projetée dans une bassine de liquide, elle finit irrémédiablement par fusionner avec le liquide ; on parle alors de coalescence. En revanche, si la bassine vibre verticalement, la goutte d’eau peut éventuellement rebondir indéfiniment. Intrigant ? Il y a mieux !
Si la bassine vibre de manière suffisamment intense, des ondes apparaissent spontanément à la surface du liquide et la goutte rebondissante se met à avancer, « à marcher sur un liquide » ! Surprenant non ? Je vous propose tout d’abord de vous expliquer comment un tel phénomène se produit. Et dans un second temps, je discuterai quelques propriétés fascinantes de ces objets, appelés marcheurs.
Faire rebondir une goutte sur un liquide
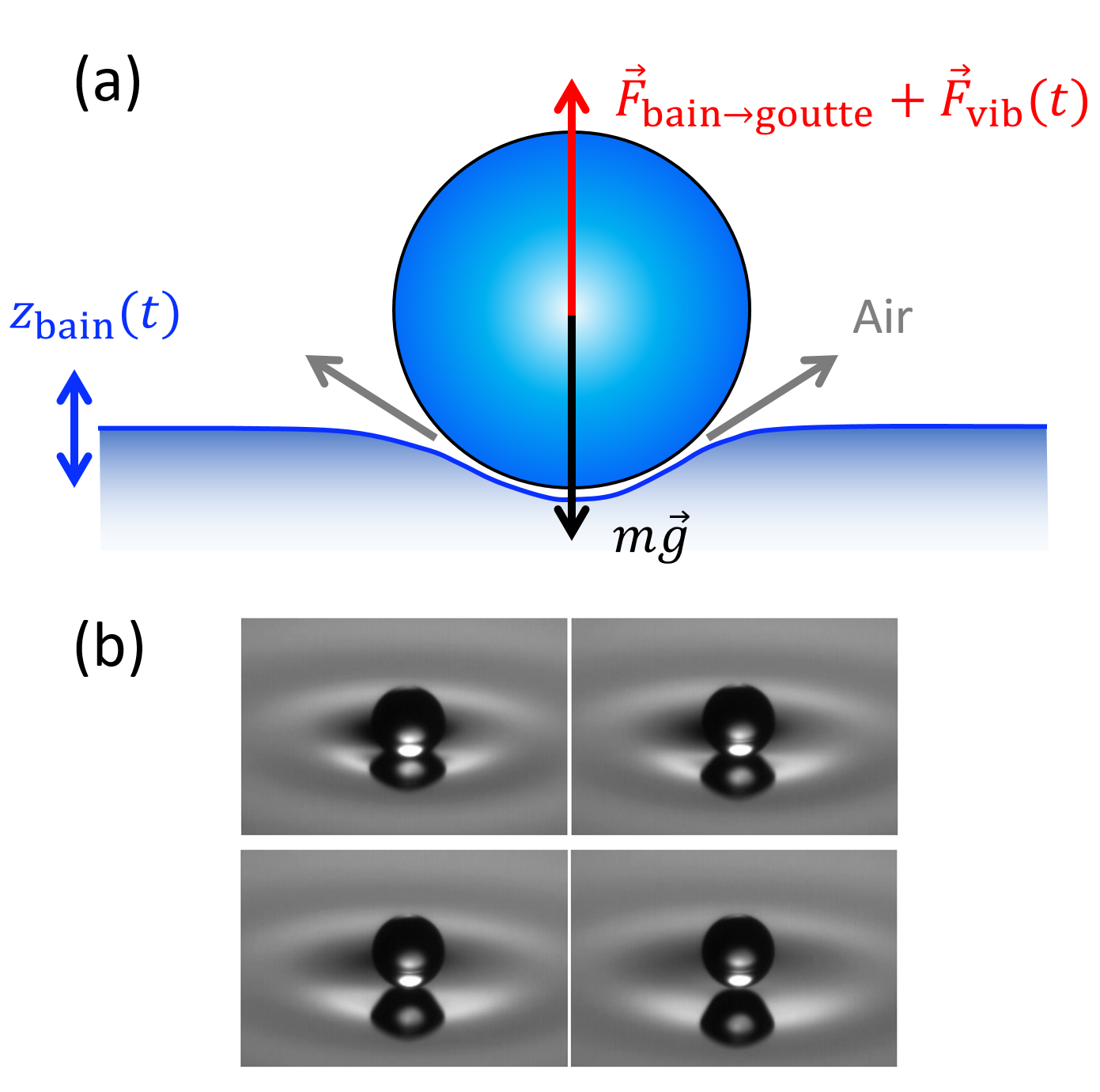
Il faut tout d’abord s’attarder un peu plus sur cet événement apparemment banal, une goutte impactant une surface du même liquide. À y regarder de plus près, ce processus n’est pas instantané et est plus complexe qu’il n’y paraît. Imaginons une goutte arrivant à la surface d’un bain du même liquide comme schématisé sur la figure 1a. Dans les tout derniers instants avant impact, il faut que l’air entre la goutte et la surface du liquide soit expulsé, ce qui n’est pas immédiat. Pour donner un ordre de grandeur, la couche d’air à expulser est de l’ordre du dixième de millimètres. Le drainage de cet air interstitiel est d’autant plus long, qu’à ces échelles de taille, le caractère visqueux de l’air devient prépondérant. Le drainage peut durer jusqu’à plusieurs millièmes de seconde. Pendant cette expulsion de l’air, la goutte continue de tomber sous l’effet de la gravité, ce qui exerce une force sur le bain et en déforme la surface. En retour, le bain exerce donc une force sur la goutte \(\overrightarrow{F}_\mathrm{bain\rightarrow goutte}\) et ce jusqu’à la coalescence.
Si le bain vibre verticalement, la situation est différente 2. La vibration induit une succession d’accélérations et décélérations à la surface du bain, ce qui se traduit par l’ajout d’une force oscillante supplémentaire \(\overrightarrow{F}_\mathrm{vib}(t)\). La force exercée par le bain oscillant sur la goutte à l’approche du bain vaut donc \(\overrightarrow{F}_\mathrm{bain\rightarrow goutte} + \overrightarrow{F}_\mathrm{vib}(t)\). Cette force peut éventuellement excéder la force de pesanteur et éjecter la goutte vers le haut 3 . Elle décolle donc, atteint un maximum d’altitude puis redescend vers le bain. À l’approche de ce dernier, le bain exerce une force sur la goutte qui peut excéder la force de pesanteur, elle redécolle et ainsi de suite. Qualitativement, la situation est semblable à une balle rebondissant sur un plateau vibrant verticalement, à la différence près que la goutte cesse d’exister si la vibration est coupée . La figure 1b montre le rebond d’une goutte d’une huile silicone (cette huile est ici \( 50 \) fois plus visqueuse que l’eau) à la surface d’un bain vibré du même liquide. La goutte (de diamètre légèrement inférieur au millimètre) rebondit alors avec une période de \( T_F = 25~\mathrm{ms} \) et le bain oscille deux fois plus rapidement avec une amplitude d’accélération égale à \( 4.5~\mathrm{g} \). Dans ce régime de paramètres, le rebond vertical de la goutte se synchronise avec l’oscillation verticale du bain.
Propulser une goutte à la surface d’un liquide
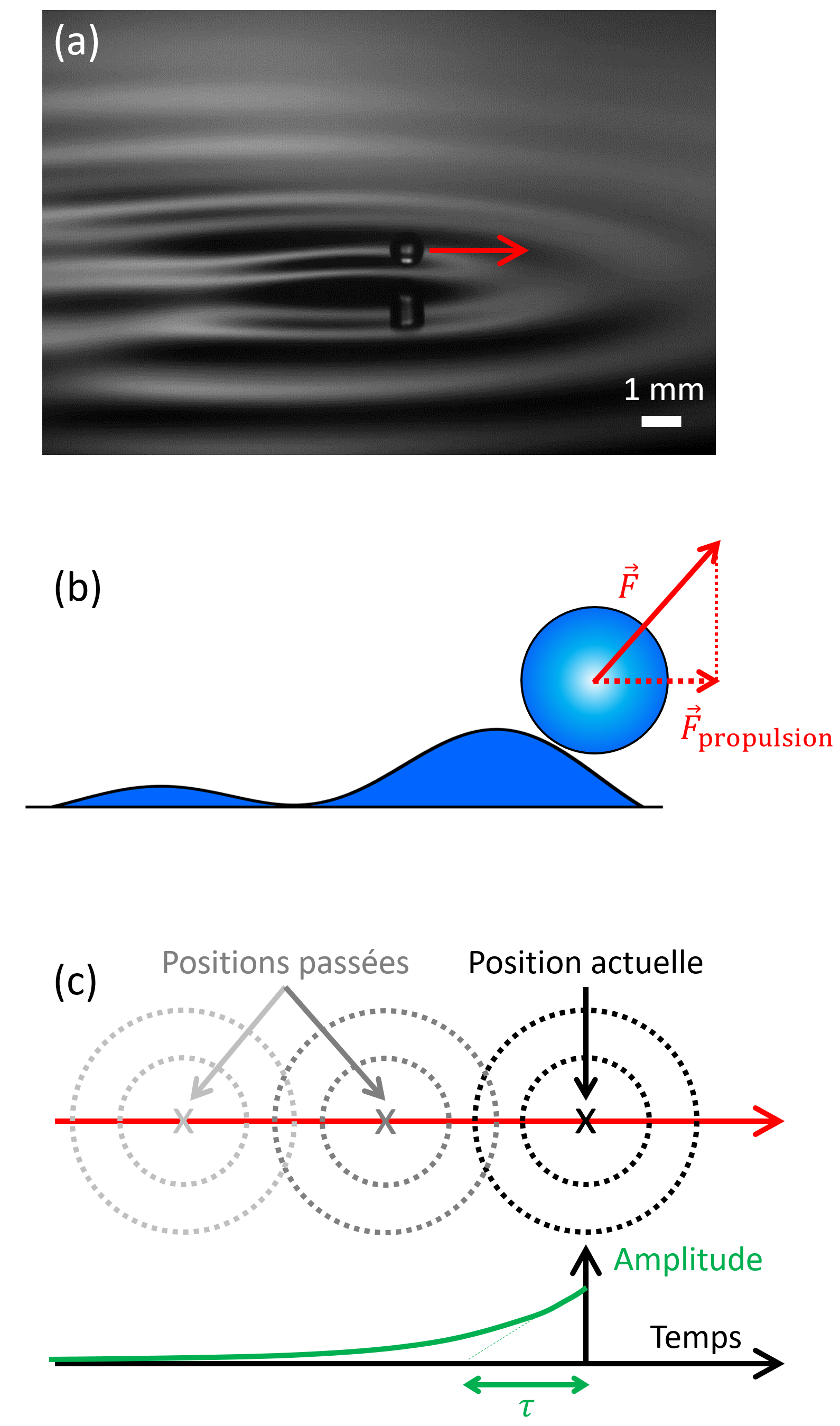
En augmentant un peu l’amplitude d’accélération, disons jusqu’à \( 4.8~\mathrm{g} \), des ondes de surface localisées près de la goutte surgissent spontanément et cette dernière se met à avancer en ligne droite dans le plan horizontal (voir figure 2a) avec une direction initiale aléatoire 4–6. Elle avance jusqu’à atteindre les bords du bain, se réfléchit et repart dans une autre direction. Comment ce mouvement spontané est-il possible ? D’où viennent ces ondes de surface et en quoi sont-elles liées à la propulsion de la goutte ?
Habituellement, une interface entre un liquide au repos et de l’air est plate et horizontale. En revanche, si l’on fait vibrer un bain verticalement cet état devient instable au-delà d’un seuil critique d’accélération, dit seuil d’accélération de Faraday, du nom d’un physicien britannique du 19e siècle. Je vous recommande d’aller regarder la vidéo suivante afin d’avoir un aperçu du phénomène. Une interface liquide/air peut également propager des ondes dont les propriétés de propagation dépendent et la tension de surface de l’interfacea et de la gravité. Dès lors que l’on module un paramètre, dans notre cas la gravité apparenteb à la surface du bain oscillant, ce système oscillatoire peut devenir instable. Cette instabilité dite paramétrique se retrouve dans de nombreux domaines de la physique, de la mécanique à l’optique en passant par la physique des plasmas. Mais revenons à notre cas. Au-delà du seuil critique de Faraday, une onde stationnaire envahit l’ensemble de la surface du liquide, en deçà l’interface est plate. Néanmoins si l’on se place légèrement sous le seuil de l’instabilité et que l’on perturbe la surface par l’impact d’une goutte, les modes instables se réveillent et survivent en décroissant pendant un certain temps moyen ? que l’on appelle temps de mémoire. Ce temps de mémoire est d’autant plus long que l’accélération du bain se rapproche du seuil d’accélération de Faraday. Au rebond suivant, la goutte atterrit sur une surface qui n’est plus tout à fait plane ce qui la propulse vers l’avant (voir figure 2b). Au rebond suivant, rebelote ! Le nouvel impact génère une onde s’ajoutant à ce qu’il reste des ondes générées un rebond plus tôt et ainsi de suite. Comme schématisé sur la figure 2c, l’onde stationnaire de surface dépend donc de la position du dernier impact, mais également des précédents. Le rapport \( \tau / T_F \) indique le nombre moyen de rebonds que le système ondulatoire se remémore. On l’appelle donc la mémoire ondulatoire du système 7.
Propriétés de quantification d’un système onde-pilote macroscopique
Il s’agit d’un système dynamique hors d’équilibre pour le moins intrigant : la goutte a besoin de l’onde pour avancer tandis que l’onde a besoin de l’impact de la goutte pour être générée. En raison de cette interdépendance entre la goutte et son onde compagnon, on dit que ce système est dual. Cette dualité onde-particule à l’échelle macroscopique est une propriété originale, car elle fait écho aux idées portées par Louis de Broglie au début de la construction de la théorie quantique du début du 20e siècle c. Cette propriété singulière a motivé un certain nombre de physiciens à creuser la question (dont moi-même, durant ma thèse de doctorat). Il ne s’agit pas d’un système quantique, mais ce système, stockant de l’information sous forme ondulatoire, possède une mémoire propre permettant d’obtenir des corrélations internes à temps longs, notamment dans les régimes de haute mémoire ondulatoire dans lesquels on se place pour la suite.
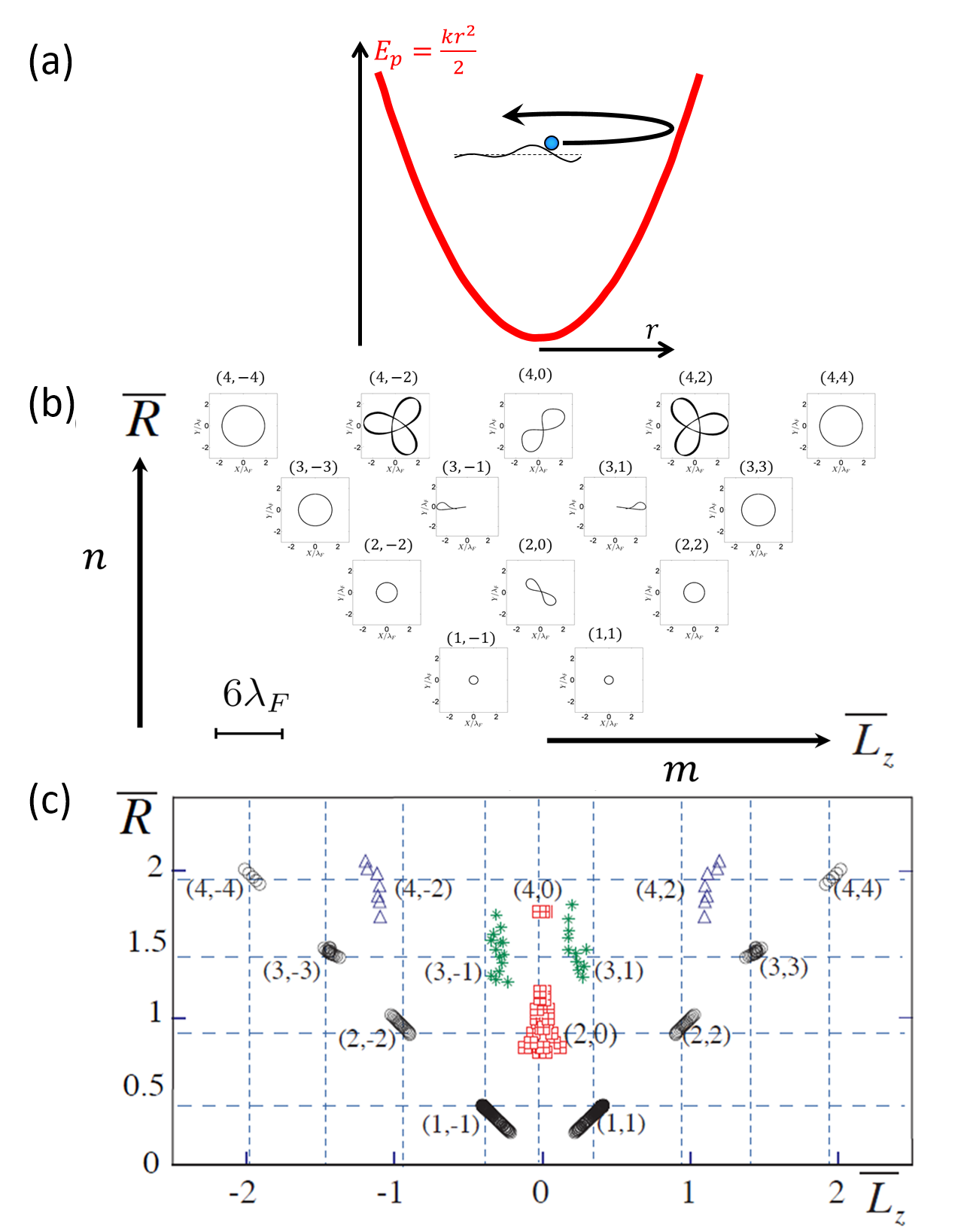
Une des principales conséquences de ces corrélations internes est la « quantification » des trajectoires suivies par le marcheur. Lors de ma thèse, avec Stéphane Perrard, nous avons étudié les trajectoires de marcheurs dans des pièges bidimensionnels dits harmoniques comme schématisés sur la figure 3a (Stéphane expérimentalement, moi théoriquement et numériquement). Nous avons découvert qu’en changeant la raideur de confinement, la forme des trajectoires changeait par saut discret. Comme résumé sur la figure 3b, il peut s’agir de trajectoires circulaires tournant autour du centre du piège harmonique, mais également de trajectoires avec des symétries d’ordre plus élevé. Ces trajectoires numériques sont classifiées en fonction de leur extension moyenne \( \overline{R} \) et de leur état de rotation (moment angulaire moyen) \( \overline{L}_z \) d. La figure 3c nous montre clairement cette double quantification dans la mesure où l’ensemble des trajectoires stables forme un ensemble discret.
L’émergence d’une double quantification, en taille et en état de rotation, repose ici sur des phénomènes d’autoadaptation entre des trajectoires et le champ d’onde de surface. Le mécanisme complet est complexe, mais l’idée essentielle est la suivante. Comme schématisé sur la figure 3b, les trajectoires stables sont des trajectoires périodiques, ce sont donc des trajectoires fermées. Sur une trajectoire fermée, chaque impact génère des ondes stationnaires cylindriques centrées aux points d’impact successifs (de manière comparable à la figure 2c). La superposition de toutes ces ondes forme un motif ondulatoire bien défini (que l’on appelle un mode) que la goutte revisite au tour d’orbite suivant. Plus la sommation est constructive et plus la force de confinement est importante ce qui pousse la goutte à se rapprocher des nœuds e du mode. Tant qu’elle reste dans cette situation, elle continue sa trajectoire. Si elle s’écarte trop du nœud, l’amplitude du mode de confinement croît ce qui ramène la goutte à sa position initiale. Une description un peu plus détaillée ce mécanisme d’auto-organisation ondulatoire peut être trouvée dans les articles suivants 8–14.
Conclusion
Il est assez frappant de voir qu’en partant d’un événement apparemment aussi banal qu’une goutte d’eau impactant un liquide, on peut aboutir à un tel système de marcheurs. Dans certaines conditions, une goutte de liquide peut rebondir sur un bain du même liquide. Plus impressionnant encore, une goutte de liquide peut se déplacer à la surface sur un bain du même liquide. J’ai essayé de vous décrire quelques propriétés des marcheurs, notamment le caractère dual de leur dynamique et la quantification de leurs trajectoires en piège harmonique. Leurs propriétés de mémoire en font des objets tout à fait originaux dans la mesure où leur dynamique interne est non locale en temps. Les marcheurs suscitent la fascination de nombreuses équipes de recherches à travers le monde, et leur étude a permis des cheminements de pensées tout à fait inattendus qui à leur tour ont donné lieu à des applications nouvelles comme dans le contrôle ondulatoire 15.
La description du système est issue du travail de thèse de Susie Protière puis Antonin Eddi. Le travail en confinement harmonique a été réalisé lors de ma thèse de doctorat encadrée par Emmanuel Fort (Institut Langevin, ESPCI), co-encadrée par Yves Couder (MSC Univ. Paris Diderot) et John Bush (Math. Dpt, MIT). Mon travail a été principalement théorique et numérique. L’ensemble des résultats expérimentaux a été obtenu lors de la thèse de Stéphane Perrard avec qui j’ai étroitement collaboré.
Notes
| a. | ↑ | Statistiquement, une molécule a moins de voisines à une interface liquide/gaz qu’en volume. Ce déficit local d’interactions à une interface liquide/gaz a donc un coût énergétique à l’origine d’une tension dite de surface. |
| b. | ↑ | En vibrant le bain, ce dernier accélère puis décélère périodiquement. Chacune de ses phases d’accélération et décélération revient à modifier la gravité effectivement ressentie par le fluide. |
| c. | ↑ | Aux petites échelles les particules ont des comportements ondulatoires et leurs états sont décrits par les règles de la mécanique quantique. |
| d. | ↑ | Le moment angulaire d’une particule de masse \(m \) à une distance \( r \) du centre de rotation et à la vitesse orthoradiale \( v \) vaut \( mrv \). Il s’agit d’une quantité intéressante dans les mouvements de rotation, car conservée dans le cas de forces centrales, comme pour une planète en orbite, pour un électron autour d’un proton, etc… |
| e. | ↑ | Un nœud d’un mode est l’endroit où le champ est nul. |









