La Terre possède un champ magnétique, et heureusement ! Celui-ci agit en effet comme un bouclier qui nous protège d’un bombardement constant par les particules de vent solaire. Mais elle n’est pas le seul corps céleste dans ce cas : le Soleil possède également son propre champ magnétique, tout comme de nombreuses planètes, étoiles et galaxies. L’origine et la persistance de ces champs magnétiques astrophysiques posent encore beaucoup de questions fondamentales.
Mais d’où viennent les champs magnétiques célestes ?
Depuis le 19e siècle, et notamment grâce aux travaux de Carl Friedrich Gauss, les mesures toujours plus nombreuses de l’orientation et de l’intensité du champ magnétique terrestre à la surface ont permis de montrer que celui-ci trouve son origine à l’intérieur de la Terre. On pourrait imaginer la présence d’un aimant géant au centre de la Terre… Cette piste est cependant exclue en raison des températures qui y règnent : n’importe quel aimant perd son aimantation s’il est chauffé au-delà d’une certaine température, appelée température de Curiea. La piste d’un champ magnétique fossileb, encore retenue pour certaines étoiles, est également exclue dans le cas de la Terre. Les paléo-champs enregistrés au cours des temps géologiques par les roches volcaniques témoignent en effet d’une intensité presque constante depuis environ trois milliards d’années… Or un champ magnétique baignant dans un milieu conducteur d’électricité est, en l’absence de source pour le régénérer, détruit par effet Joule : l’énergie magnétique est alors progressivement dissipée sous forme de chaleur, et finit par s’épuiser au bout d’un temps caractéristique déterminé par la taille du domaine et sa conductivité électrique – ce qui dans le cas de la Terre aurait dû se produire en moins de 100 000 ans !
Il existe donc un mécanisme à l’œuvre dans certains corps astrophysiques pour entretenir ce champ magnétique malgré la dissipation par effet Joule. Et nous savons que ce mécanisme possède une dynamique compliquée : la migration au cours du temps du pôle Nord magnétique indiqué par la boussole, les renversements Nord-Sud que le champ magnétique a subis dans le passé, et dont les roches volcaniques ont gardé la trace, mais aussi dans le cas du Soleil l’activité fluctuante des taches solaires (déjà observées par Galilée !)… tous ces éléments sont autant de signatures de la complexité du processus.
Depuis environ un siècle, l’hypothèse retenue par les physiciens est celle d’un champ magnétique entretenu par effet dynamo dans de nombreux corps célestesc. Un peu comme dans une dynamo de vélo, qui transforme l’énergie mécanique associée au mouvement des roues en énergie électrique ! Mais dans les planètes ou les étoiles, ou encore dans le milieu galactique, la source d’énergie mécanique provient des mouvements d’un fluide conducteur d’électricité – métal liquide ou plasma par exemple -, ces mouvements pouvant eux-mêmes être influencés par le champ magnétique qu’ils entretiennent (ce qui ne s’applique évidemment pas au vélo).
Comment opère la dynamo ?
En effet, un champ magnétique et un écoulement de fluide conducteur d’électricité connaissent une évolution couplée, décrite par les équations de la magnétohydrodynamique. Le champ magnétique agit à travers la force de Laplace sur les mouvements du fluide porteur de charges électriques, tandis que ceux-ci induisent des courants électriques qui peuvent à leur tour régénérer le champ magnétique. Mais pour que le processus soit auto-entretenu, autrement dit pour que le champ magnétique puisse se maintenir malgré la dissipation par effet Joule, les mouvements du fluide doivent être favorables, ce qui en pratique signifie qu’ils doivent être à la fois suffisamment compliqués et suffisamment vigoureux pour permettre à la dynamo d’opérer.
D’où viennent alors ces mouvements “compliqués et vigoureux” ? Il est malheureusement très difficile d’exhiber par la théorie un écoulement capable d’engendrer une dynamo. Dans les étoiles et les planètes, les scénarios les plus largement étudiés invoquent un brassage par convection d’une enveloppe fluide conductrice d’électricité, qu’il s’agisse d’un noyau de métal liquide, d’une atmosphère d’hydrogène métallique, ou encore du plasma d’une étoile : le fluide, plus chaud et léger en profondeur, remonterait en direction de la surface, puis se refroidirait et retomberait sous forme de panaches. Les simulations numériques tendent à montrer que ces mouvements de convection seraient en effet capables d’entretenir dans une coquille sphérique en rotation des champs magnétiques morphologiquement semblables à ceux de la Terre, de Jupiter ou encore du Soleil.
Cependant, les modèles de dynamos convectives se heurtent à un certain nombre de limitations : présence incertaine de convection dans les intérieurs planétaires, incompatibilité avec certains corps astrophysiques de trop petite taille (comme les lunes de Jupiter Io et Ganymède, ou encore la Lune primitive), difficulté à rendre compte de la très grande diversité des champs magnétiques stellaires observés (par exemple, comment expliquer l’énorme différence d’intensité du champ magnétique entre étoiles massives ?)… Toutes ces raisons contribuent à motiver la recherche de scénarios alternatifs pour l’émergence d’une dynamo en géométrie sphérique, sans avoir recours à l’hypothèse de convection.
Un ingrédient omniprésent : la rotation différentielle
Le scénario que nous proposons dans notre travail de recherche1 repose sur un écoulement particulier qui peut se développer dans un fluide tournant à une vitesse différente selon sa distance à l’axe de rotation – on parle alors de rotation différentielle. La rotation différentielle est omniprésente en astrophysique – dans les disques d’accrétion, les atmosphères planétaires ou les intérieurs stellaires : ainsi, des mesures effectuées par la sonde spatiale SoHO ont très récemment permis de montrer que le cœur du Soleil tourne beaucoup plus vite que son enveloppe extérieure !2 Il est donc naturel de s’intéresser aux possibles processus dynamo exploitant ce mécanisme…
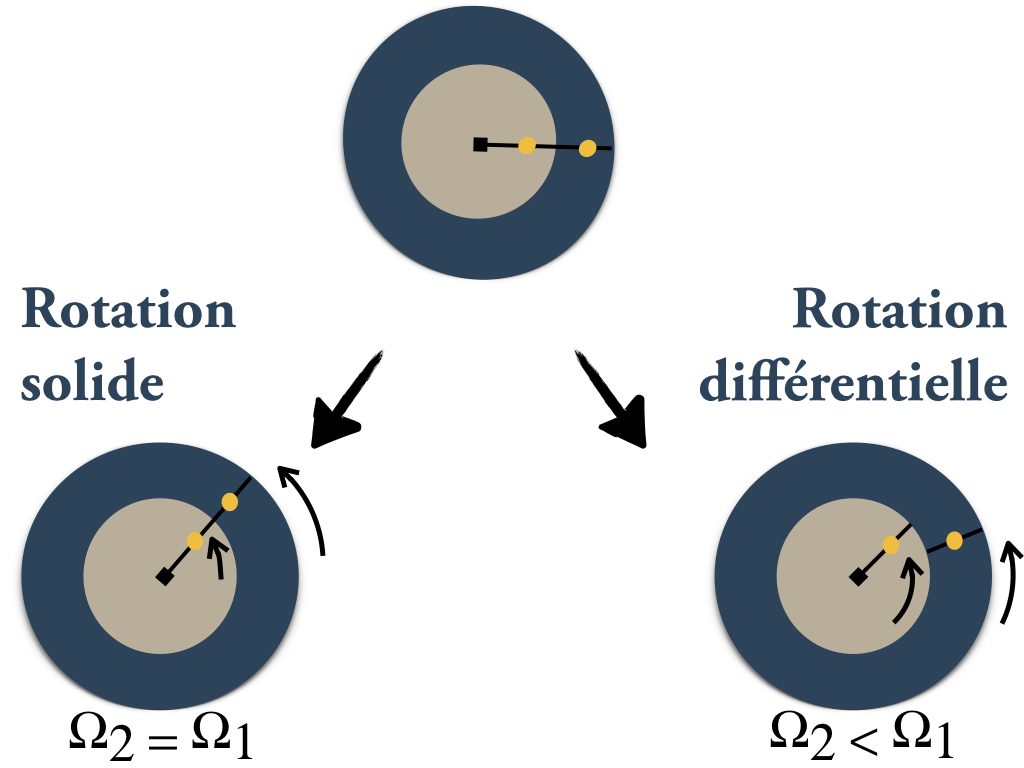
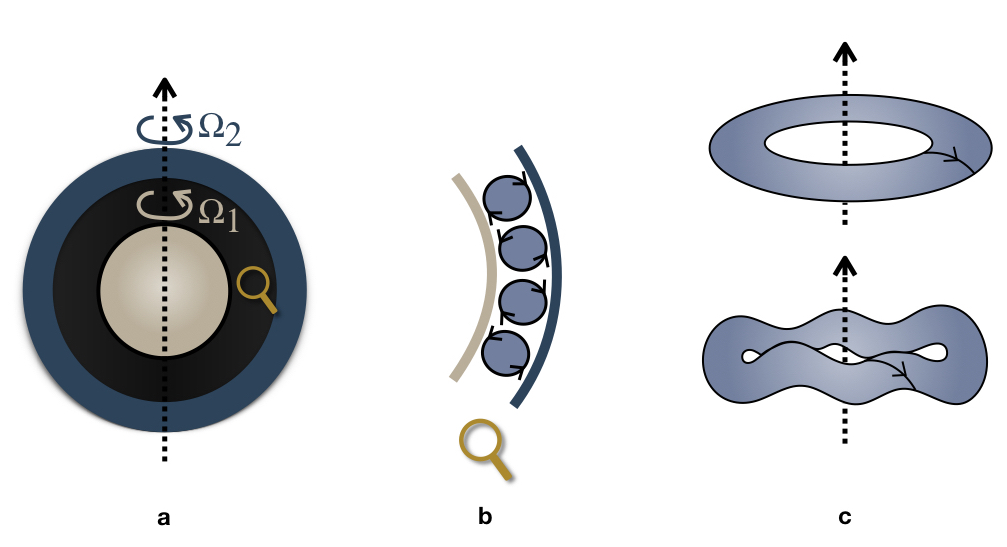
Considérons maintenant un fluide contenu dans un espace fin entre deux sphères en rotation à des vitesses angulaires différentes (comme sur le schéma en figure 2). Si la sphère interne tourne plus vite que la sphère externe, et si la différence de vitesse angulaire \(\Delta\Omega\) entre les deux dépasse une certaine valeur critique \(\Delta\Omega_c\), des tourbillons se développent dans le fluide sous l’effet de la force centrifuge. Ces tourbillons prennent la forme de rouleaux toriques, localisés dans la région équatoriale, et que l’on appelle les rouleaux de Taylor-Couette. (Voir le schéma en figure 2b. On peut observer les mêmes rouleaux dans une coquille cylindrique, comme sur la vidéo de cette expérience :
Dans le cas du cylindre, les tourbillons se forment sur toute la hauteur du fluide, tandis que dans la sphère ils se concentrent près de l’équateur, c’est-à-dire là où les parois sont quasiment verticales). Lorsque la différence de vitesse angulaire entre les deux sphères augmente encore, les rouleaux de Taylor-Couette commencent à présenter des ondulations dans la direction azimutale (voir schéma en figure 2c), puis leur structure se complique encore à mesure que l’écoulement devient de plus en plus turbulent.
La dynamo de Taylor-Couette sphérique
Dans un article récent1, nous montrons à l’aide de simulations numériques qu’en présence d’un champ magnétique, les tourbillons de Taylor-Couette sont justement capables d’engendrer une dynamo dans une enveloppe sphérique. Lorsque la différence de vitesse angulaire \(\Delta\Omega\) entre les deux sphères est inférieure à la valeur critique \(\Delta\Omega_c\), donc trop faible pour observer les tourbillons, le champ magnétique baignant initialement dans le fluide est toujours dissipé par effet Joule et la dynamo n’opère pas. Mais lorsque cette différence de vitesse augmente et que les tourbillons apparaissent, nous pouvons obtenir une dynamo dès que les effets de dissipation du champ magnétique sont suffisamment faibles par rapport à ceux du brassage du fluide par les rouleaux. En pratique, cela signifie qu’une graine de champ magnétique initialement très faible voit alors son énergie magnétique croître exponentiellement, dans un premier temps. Lors de cette phase de croissance exponentielle, le champ magnétique est encore trop faible pour que sa rétroaction sur l’écoulement se fasse sentir. Mais lorsqu’il devient assez fort pour influencer à son tour significativement les mouvements du fluide conducteur, ceux-ci s’adaptent de manière à “stopper” sa croissance (sinon l’énergie magnétique deviendrait infinie !) : on parle de saturation. L’énergie magnétique atteint alors sa valeur maximale, autour de laquelle elle se maintient par la suite avec plus ou moins de fluctuations.

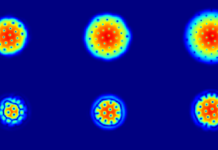
Dans le cas de la dynamo de Taylor-Couette sphérique, le champ magnétique ainsi entretenu est essentiellement concentré dans la région équatoriale, au niveau des tourbillons (voir figure 3). Lorsqu’il devient suffisamment fort, il déforme les tourbillons qui présentent alors des ondulations azimutales semblables à celles observées, même en l’absence de champ magnétique, pour une différence de vitesse angulaire \(\Delta\Omega\) suffisamment grande (comme sur le schéma en figure 2c). Et de manière surprenante, la dynamo semble particulièrement efficace lorsque le nombre d’ondulations fabriquées par le champ magnétique dans les rouleaux est le même que celui spontanément présenté par les rouleaux en l’absence de champ magnétique pour le même \(\Delta\Omega\) – il s’agit d’un phénomène de résonance.
Bien évidemment, aucune simulation numérique n’est capable à ce jour de modéliser des écoulements aussi complexes et aussi turbulents que ceux qui règnent vraisemblablement dans les intérieurs planétaires ou stellaires : nous ne pouvons donc que supposer une certaine robustesse du mécanisme observé dans les régimes pertinents pour les objets astrophysiques… Dans ce nouveau modèle de dynamo, l’ingrédient-clé est l’existence d’une zone, même très étroite, dans laquelle le fluide conducteur se trouve en rotation différentielle. Il faut enfin qu’à travers cette région, la vitesse de rotation décroisse suffisamment fort vers l’extérieur pour que les rouleaux puissent s’y développer. Or, les données d’astéro-sismologie dont nous disposons à l’heure actuelle montrent déjà que certaines étoiles présentent justement des profils de rotation a priori compatibles ! Et si la présence effective de rouleaux de Taylor-Couette dans un intérieur stellaire reste encore hypothétique, il est néanmoins possible d’imaginer un scénario dans lequel les rouleaux engendreraient une dynamo au cœur de ces étoiles.
Notes
| a. | ↑ | Les températures estimées pour le noyau terrestre, supérieures à 3800°C (http://www.insu.cnrs.fr/node/4357), excèdent largement la température de Curie des matériaux qui le constituent principalement (fer et nickel). |
| b. | ↑ | Voir aussi un article précédent du Rayon par Jean-Baptiste Durrive. |
| c. | ↑ | D’abord formulée en 1919 par Joseph Larmor au sujet du Soleil, cette hypothèse a été ensuite étendue à la Terre et à de nombreux objets astrophysiques (étoiles, planètes, galaxies, etc.). |









Excellente presentation. Merci
Fine way of explaining, and good paragraph to take data on the topic
of my presentation topic, which i am going to present in university.