Parmi toutes les planètes de l’Univers, la communauté scientifique estime que certaines sont co-orbitales. C’est-à-dire, sans entrer dans les détails, qu’elles partagent une même orbite autour de leur étoile. C’est en tout cas ce que l’on pensait jusqu’à ce que les télescopes nous permettent de découvrir de nombreuses planètes hors du système solaire, sans jamais trouver la moindre paire de planètes co-orbitales. Aujourd’hui, après des milliers de découvertes, les planètes co-orbitales manquent toujours à l’appel, et j’explique dans cet article comment les marées peuvent être responsables de leur destruction, élucidant le mystère des planètes co-orbitales introuvables.
Les exoplanètes
Commençons par définir des termes. Déjà, c’est quoi une exoplanète ? L’union astronomique internationale définit une planète comme un corps céleste orbitant autour du Soleil, suffisamment massif pour être sphériquea et pour dominer son orbite. Le système solaire compte huit planètes, et toutes sont connues depuis la découverte de Neptune en 1846 par Urbain Le Verrier.
Une exoplanète, c’est tout simplement une planète en orbite autour d’une étoile autre que le Soleil. Rien que dans notre galaxie, la Voie lactée, on estime à 400 milliards le nombre d’exoplanètes. Autant dire qu’on ne parle pas de quelque chose de rare. Et pourtant, leur détection est très ardue en raison de la distance qui nous sépare d’elles. En effet, les exoplanètes sont presque toutes situées à plus de 10 années-lumière de la Terre, et sont rarement plus grandes que Jupiter. Or, observer une exoplanète de la taille de Jupiter située à seulement 10 années-lumière revient à observer un moucheron de 5 mm situé à 7400 km ! De plus, ces planètes sont en orbite autour de leur étoile, considérablement plus grande et brillante qu’elles, si bien que finalement, observer une exoplanète, c’est, dans le meilleur des cas, regarder depuis les États-Unis un moucheron qui tourne autour d’un lampadaire parisien. Ainsi, on n’observe presque jamais directement une exoplanète. Mais heureusement, des méthodes indirectes permettent de les détecter. La plus facile à comprendre est celle des transits. Si par chance l’exoplanète orbite autour de son étoile perpendiculairement au ciel, alors elle passe périodiquement devant cette dernière et les éclipses qu’elle provoque peuvent être détectées en mesurant la luminosité de l’étoile hôte au cours du temps. L’effet Doppler, qui sert à mesurer la vitesse d’un véhicule au radar, ou la vitesse radiale d’une étoile, a aussi permis la détection indirecte de beaucoup d’exoplanètes. Ces deux méthodes de détection sont illustrées en Figure 1. Au 6 octobre 2023, ce sont ainsi 5506 exoplanètes orbitant autour de 4064 étoiles qui ont été découvertes.

Le mouvement co-orbital
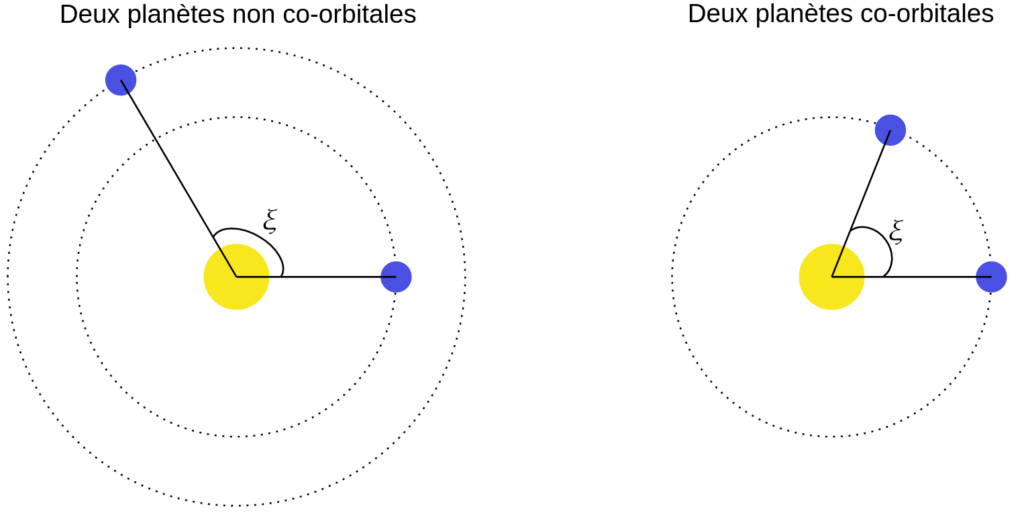
Maintenant, dans quelles circonstances dit-on que deux planètes sont co-orbitales ? Simplement, on peut dire que deux planètes sont co-orbitales quand elles partagent des orbites similaires, mais cette définition est restrictive et peu précise. Une meilleure définition consiste à dire que deux planètes sont co-orbitales si l’angle qu’elles forment avec l’étoile ne s’annule jamais, c’est-à-dire, si ces deux planètes orbitent en moyenne à la même vitesse. Grâce à la troisième loi de Kepler, on sait que la vitesse orbitale d’une planète est d’autant plus petite qu’elle orbite loin de l’étoile, et donc, pour que deux planètes soient co-orbitales, il faut qu’elles orbitent autour de leur étoile à des distances semblables. J’illustre en Figure 2 cette définition. À gauche, les deux planètes ne sont pas co-orbitales, tandis qu’à droite, elles le sont.
Le cas de gauche en Figure 2 correspond par exemple, dans le système Solaire, au couple Terre–Mars autour du Soleil. Tandis que la Terre complète une révolution du Soleil en 1 an, Mars prend 1,88 ans, et tous les 26 mois environ, la Terre rattrape Mars dans son orbite et l’angle \(\xi\) s’annule : c’est l’opposition. La Terre et Mars ne sont donc pas co-orbitales, et en fait, dans le système Solaire, il n’existe pas de planètes co-orbitales.
À ce stade de la discussion, on pourrait se dire que si on ne détecte pas d’exoplanètes co-orbitales, c’est peut-être tout simplement parce qu’elles n’existent pas. Dans le système solaire cependant, malgré l’absence de couple de planètes co-orbitales, on a découvert des satellites de Saturne co-orbitaux, et de nombreux astéroïdes (non moins de 12 143) sont co-orbitaux à Jupiter. Sans aucune observation, Joseph-Louis Lagrange a découvert par le calcul en 1772 une configuration co-orbitale intéressante. Si l’angle \(\xi\) vaut 60◦, alors les deux planètes sont immobiles l’une par rapport à l’autre, c’est-à-dire qu’elles forment avec l’étoile un triangle équilatéral tournant à vitesse constante. Cette configuration est l’équilibre équilatéral de Lagrange. Le fait que les deux planètes soient immobiles l’une par rapport à l’autre signifie que si l’on observe le système en tournant avec une planète, l’autre est fixe, et c’est la raison pour laquelle la configuration équilatérale est un équilibre relatif du problème des trois corps, c’est à dire un équilibre dans un référentiel non inertiel. Toutefois, il existe des configurations co-orbitales qui ne sont pas des équilibres.
Dans la Figure 3, je représente des trajectoires co-orbitales possibles, affichées dans un repère qui tourne avec l’une des planètes (le petit point noir à droite). Ces trajectoires (obtenues par Yoder et al.1, après le survol des satellites co-orbitaux de Saturne par Voyager 1) sont calculées en déterminant les lignes de niveau de l’énergie, comme dans la Figure 4.
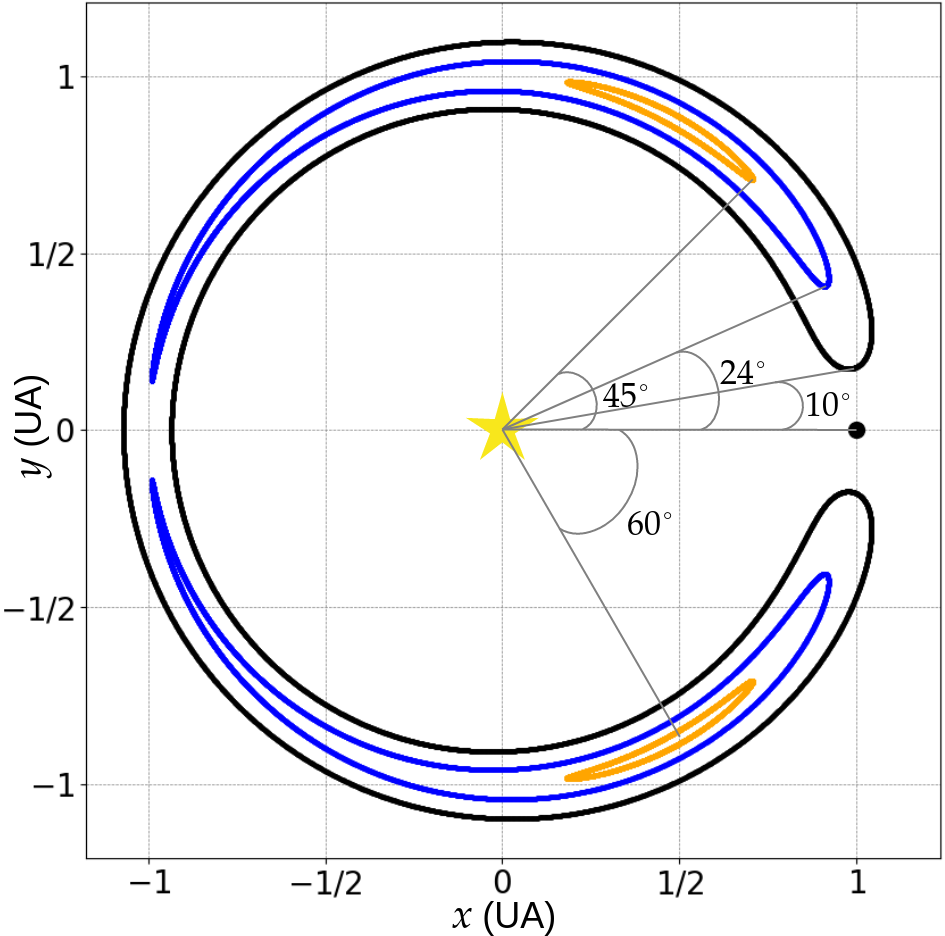
Suivant la trajectoire, l’angle \(\xi\) entre les planètes oscille plus ou moins, au gré de l’interaction gravitationnelle mutuelle. Tandis que les planètes ne s’approchent pas à moins de 45◦ pour les trajectoires oranges, elles s’approchent à seulement 10◦ dans la trajectoire noire. On observe deux types d’orbites, selon la valeur minimale atteinte par l’angle \(\xi\). Pour \(\xi_\text{min}\) > 23.9◦ (orange et bleu), les trajectoires, confinées dans le demi-plan supérieur ou inférieur, sont appelées orbites troyennes. Au contraire, pour \(\xi_\text{min}\) < 23.9◦ (noir), les trajectoires sont beaucoup plus étendues et prennent le nom d’orbites en fer-à-cheval, en raison de leur forme caractéristique. Toutes ces trajectoires, qu’elles soient troyennes ou en fer-à-cheval, sont parcourues en un temps bien plus long que la période de révolution. Par exemple, Janus et Épiméthée, deux satellites co-orbitaux de Saturne, parcourent leur fer-à-cheval en 4 ans, alors qu’ils complètent une révolution autour de Saturne en seulement 17 heures.
Plus l’angle \(\xi\) oscille, plus les planètes co-orbitales se rapprochent quand \(\xi\) atteint son minimum. Si l’angle \(\xi\) diminue trop, c’est à dire si les co-orbitaux sont sur un fer-à cheval trop refermé, alors les planètes s’approchent trop et leur interaction gravitationnelle mutuelle les fait entrer en collision, ou détruit la configuration co-orbitale. Plus les planètes sont massives et moins elles peuvent s’approcher sans détruire la configuration co-orbitale. Si on appelle \(\varepsilon\) (lire epsilon) le rapport entre la masse totale des deux planètes et celle de l’étoile, alors il existe une valeur maximum de \(\varepsilon\) telle qu’une trajectoire co-orbitale donnée soit stable. Appelons \(m_0\) la masse de l’étoile et \(m_1\) et \(m_2\) les masses des planètes co-orbitales. Le rapport \(\varepsilon\) s’écrit alors \(\varepsilon=\frac{m_1+m_2}{m_0}\) et pour que les orbites montrées en Figure 3 ne soient pas instables, Leleu et al.2 ont déterminé à l’aide de simulations numériques qu’il faut que
- \(\varepsilon\) < 0.034 pour l’équilibre équilatéral (\(\xi_\text{min}\) = 60◦), démontré par le calcul par Gascheau3,
- \(\varepsilon\) < 0.0063 pour les orbites troyennes oranges (\(\xi_\text{min}\) = 45◦),
- \(\varepsilon\) < 0.00050 pour les orbites troyennes bleues (\(\xi_\text{min}\) = 24◦) et
- \(\varepsilon\) < 0.000025 pour l’orbite en fer-à-cheval noire (\(\xi_\text{min}\) = 10◦).
De manière générale, plus l’orbite co-orbitale est étendue, plus le rapport \(\varepsilon\) entre la masse planétaire totale et la masse de l’étoile doit être petit pour garantir la stabilité du système. Ces valeurs critiques pour \(\varepsilon\) peuvent sembler petites, mais elles ne sont en réalité pas contraignantes, tant les exoplanètes sont considérablement moins massives que leurs étoiles hôtes. Le mouvement co-orbital entre deux planètes est donc tout à fait possible théoriquement, et les modèles numériques de formation planétaires prédisent même que jusqu’à 12 % des systèmes planétaires devraient contenir des exoplanètes co-orbitales (Leleu et al.4, Figure 12). Pourtant, malgré la détection de 5506 exoplanètes dans 4064 systèmes planétaires différents, aucune exoplanète co-orbitale n’a été détectée à ce jour, ce qui constitue un grand mystère pour les mécaniciens célestes.
Les marées
Une hypothèse qui a été proposée face à ce mystère est que les marées sont peut-être responsables de la destruction des exoplanètes co-orbitales. Dès 2013, des études numériques ont investigué la proposition (Rodríguez et al.5), mais ce n’est pas avant 2021 qu’une étude analytique, que j’ai entreprise à l’IMCCE (Institut de mécanique céleste et de calcul des Éphémérides) avec mes directeurs de thèse Philippe Robutel et Alexandre Correia, a entériné la question. Avant de comprendre comment cela se passe, commençons par définir une marée. Contrairement aux termes définis plus tôt, celui-ci n’est pas spécifique au vocabulaire de la mécanique céleste. Tout le monde se représente une marée comme ces variations périodiques du niveau de l’océan, et en fait, c’est à peu près de ça dont il est question ici aussi.
Quand une planète orbite autour d’une étoile, le côté de la planète le plus proche de l’étoile subit une attraction gravitationnelle un peu plus intense que le côté le plus éloigné. Au gré du mouvement des deux astres, cette attraction différentielle provoque de petites déformations au sein de la planète. Une marée, c’est donc l’ensemble des déformations subies par un corps céleste en raison de l’attraction différentielle due à d’autres astres. Dans le cas de la Terre, ce sont les attractions différentielles dues au Soleil et à la Lune qui la déforment. Ce qu’il faut comprendre, c’est que la présence d’un océan n’est pas requise. Même les continents se voient déformés dans le cas des marées terrestres. Puisque l’eau des océans est moins rigide que la croûte continentale, la déformation est plus spectaculaire grâce aux océansb, mais la Terre serait toujours sujette aux marées, même sans océans.
La destruction
Une marée, ça peut mouiller la serviette d’un vacancier distrait, mais c’est quand même quelque chose d’assez inoffensif. Les déformations, de quelques mètres tout au plus, sont absolument minuscules devant la dimension d’une planète. Comment les marées pourraient alors être responsables de la destruction des exoplanètes co-orbitales? Le problème, c’est la dissipation d’énergie. Si on plie et déplie successivement une cuillère, au point de pliage, la cuillère chauffe. C’est parce que les déformations engendrées par les pliages convertissent l’énergie mécanique en énergie thermique. Les marées convertissent donc l’énergie orbitale des planètes en chaleur, elles dissipent l’énergie orbitale. La chaleur dissipée par les marées est d’ailleurs responsable du volcanisme de Io (marées levées par Jupiter) et des geysers d’Encelade (marées levées par Saturne). Les marées chauffent tellement Encelade que cette lune a un océan d’eau liquide souterrain, malgré une température de surface de −198◦C.
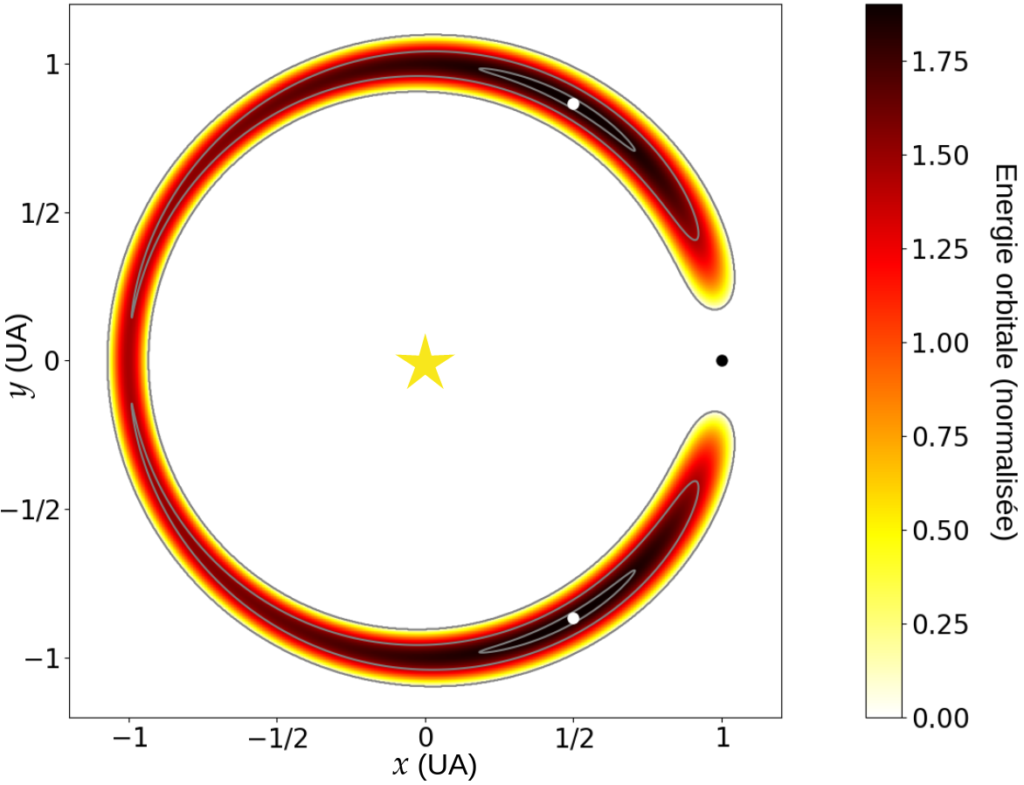
Reprenons la Figure 3 qui montrait des trajectoires co-orbitales en repère tournant, et traçons en chaque point l’énergie orbitale grâce à un code couleur : C’est la Figure 4. En l’absence de marées, l’énergie orbitale du couple d’exoplanètes n’est pas dissipée et se conserve, les trajectoires sont alors données en Figure 4 par les lignes de niveau d’énergie. Cependant, en cas de marées, l’énergie orbitale diminue progressivement en raison de la dissipation. Les trajectoires, au lieu d’être des courbes fermées, sont plutôt des spirales très serrées, comme dans l’animation en Figure 5.

D’après la Figure 4, les équilibres équilatéraux de Lagrange sont des maxima d’énergiec, et en raison de la diminution d’énergie, les trajectoires spiralent donc en dehors de ces équilibres. L’angle \(\xi\) oscille de plus en plus et les marées ont alors tendance à agrandir les trajectoires co-orbitales. En Figure 3, on passe progressivement d’une orbite orange à une orbite bleue, puis à une orbite noire. Le phénomène est sans limite et l’angle \(\xi\) entre les deux exoplanètes atteint des valeurs de plus en plus petites.
Comme on l’a vu tout à l’heure, pour une valeur donnée du rapport \(\varepsilon\) entre la masse planétaire totale et la masse stellaire, il existe une valeur minimale que peut atteindre l’angle \(\xi\) sans déstabiliser le système. Par exemple, pour que les exoplanètes puissent s’approcher à 10◦ (orbite noire en Figure 3), le rapport \(\varepsilon\) ne doit pas dépasser 0.000025. Pourtant, les marées font sans cesse diminuer la valeur minimale atteinte par \(\xi\), et le critère de stabilité sur \(\varepsilon\) finit par être rompu. Le système se déstabilise alors en raison des rencontres trop proches entre les deux exoplanètes et la configuration co-orbitale est détruite, soit par une collision, soit par l’éjection d’une exoplanète. C’est inéluctable.
Quitte à attendre suffisamment, les exoplanètes co-orbitales sont donc systématiquement détruites par les marées qu’elles subissent. Mais combien de temps ça prend ? La question est importante, car si ce temps est plus grand que l’espérance de vie de l’étoile hôte, les exoplanètes seront de toute façon détruites par l’explosion de leur étoile en géante rouge, avant de l’être par les marées, qui n’ont alors plus d’importance. Dans mon article6, j’utilise des résultats d’algèbre linéaire pour donner une expression analytique du temps de destruction. L’expression est relativement compliquée, et pour simplifier, on se limite ici au cas où les deux exoplanètes sont identiques. Appelons \(m\) leur masse commune, \(R\) leur rayon commun et \(a\) leur distance commune à l’étoile. Le temps caractéristiqued de destruction, appelé \(\tau\) (lire tau), est alors donné par la formule
\(\displaystyle{\tau=\frac{2mQa^{6.5}}{9k_2R^5\sqrt{\mathcal{G}m_0^3}}}\)
où \(\mathcal{G}\) est la constante universelle de la gravitation et \(m_0\) est la masse de l’étoile. Dans cette formule, \(k_2\) est le nombre de Love des exoplanètes, qui mesure leur capacité à se déformer sous l’effet des marées, tandis que \(Q\) est leur facteur de qualité, qui mesure leur capacité à dissiper de l’énergie quand elles sont déformées.
Calculons ce temps pour deux exoplanètes co-orbitales exactement identiques à la Terre, orbitant autour du Soleil. Le nombre de Love de la Terre vaut \(k_2=\) 0.302 et son facteur de qualité vaut \(Q=\) 280. Les autres données sont facilement consultables sur les pages Wikipédia de la Terre et du Soleil. Supposons que les exoplanètes orbitent à la distance \(a=\) 0.04 UA du Soleil, soit 6 millions de kilomètres. On remplace dans la formule et on obtient \(\tau=\) 565 millions d’années.
Ce temps, bien que plus long que le règne d’Elisabeth II, est plus court que l’âge du Soleil, qu’on estime à 4.5 milliards d’années. Ainsi, si le système solaire avait contenu à sa formation deux Terres co-orbitales à 0.04 UA, la destruction aurait déjà eu lieu.
Toutefois, le plus intéressant dans la formule qui donne \(\tau\), c’est que le temps de destruction dépend de \(a\), la distance au Soleil, à la puissance 6.5. C’est-à-dire que quand \(a\) augmente un peu, \(\tau\) augmente beaucoup. Si on double la distance à l’étoile, le temps de destruction se voit multiplié par 26.5 ≈ 90 !! Si, plutôt qu’à 0.04 UA, les deux exoplanètes sont situées à 1 UA du Soleil, qui est la véritable distance Terre–Soleil, alors \(\tau\) est multiplié par 1.22 milliards et devient faramineux. Similairement, si les deux exoplanètes orbitent autour du Soleil à 0.01 UA seulement, l’attraction différentielle est plus forte et \(\tau\) se voit divisé par 46.5 = 8192. Il ne vaut alors plus que 68 970 ans, ce qui est minuscule devant l’âge du système solaire.
Conclusion
Dans cet article, j’ai expliqué simplement comment les marées sont responsables de la destruction systématique des exoplanètes co-orbitales, ou plutôt, de la destruction de la configuration co-orbitale. Je montre aussi que le temps de destruction dépend beaucoup de la distance à l’étoile et que les marées deviennent rapidement négligeables en s’éloignant de l’étoile.
Ainsi, les marées fournissent une explication satisfaisante à l’absence de détection d’exoplanètes co-orbitales, malgré le grand nombre de détections d’exoplanètes, mais seulement pour les exoplanètes orbitant proche de leur étoile, typiquement à moins de 0.08 UA. Les exoplanètes orbitant plus loin sont immunisées contre les marées car alors, la gravitation différentielle avec l’étoile est trop faible. L’idée, c’est que la majorité des exoplanètes détectées jusqu’alors orbitent très proche de leur étoile. En effet, les méthodes de détection, comme la méthode des transits évoquée plus haut, nécessitent la complétion de plusieurs orbites pour confirmer la présence de l’exoplanète. Si l’exoplanète orbite loin, ses orbites durent plusieurs années et les télescopes sur Terre ne peuvent la détecter. Ainsi, quand on détecte une exoplanète, soit elle n’a jamais eu de compagne co-orbitale, soit elle en a eu une, mais la configuration co-orbitale a eu le temps d’être détruite par les forces de marées.
Voilà pourquoi on n’a aujourd’hui encore jamais découvert d’exoplanète co-orbitale, malgré leur existence quasi certaine. Finalement, les marées ne sont pas si inoffensives qu’elles en ont l’air.
Bibliographie
- 1 C.F. Yoder, G. Colombo, S.P. Synnott, and K.A. Yoder, “Theory of motion of saturn’s coorbiting satellites,” Icarus, 431–443 (1983).
- 2 A. Leleu, P. Robutel, and A.C.M. Correia, “Detectability of quasi-circular co-orbital planets. Application to the radial velocity technique,” A&A, A128 (2015).
- 3 M. Gascheau, “Examen d’une classe d’équations différentielles et application à un cas particulier du probleme des trois corps.,” C. R. Acad. Sci. Paris 16(7), 393 (1843).
- 4 A. Leleu, G.A.L. Coleman, and S. Ataiee, “Stability of the co-orbital resonance under dissipation,” A&A, A6 (2019).
- 5 A. Rodríguez, C.A. Giuppone, and T.A. Michtchenko, “Tidal evolution of close-in exoplanets in co-orbital configurations,” Celest Mech Dyn Astr, 59–74 (2013).
- 6 J. Couturier, P. Robutel, and A.C.M. Correia, “An analytical model for tidal evolution in co-orbital systems. I. Application to exoplanets,” Celest Mech Dyn Astr, (2021).
Notes
| a. | ↑ | Les objets célestes suffisamment massifs sont sphériques car leur propre gravitation l’emporte sur les forces de cohésion de la matière qui les compose. Ils se comportent alors comme des fluides et prennent une forme sphérique pour minimiser leur énergie potentielle. On dit alors qu’ils sont à l’équilibre hydrostatique. |
| b. | ↑ | Sur Terre, les déformations continentales sont de l’ordre de quelques dizaines de centimètres, alors qu’elles peuvent atteindre plusieurs mètres dans le cas des marées océaniques, soit des déformations de l’ordre de 0.0001 % à 0.001 %. |
| c. | ↑ | On s’attend à ce qu’un équilibre stable soit un minimum d’énergie. C’est vrai en référentiel inertiel, mais le référentiel de la Figure 4 est tournant, donc non inertiel. Il existe alors des forces d’inertie d’entraînement (c’est le nom des forces fictives qui apparaissent en référentiel non inertiel, comme la force centrifuge) telles que les équilibres de Lagrange soient des maxima d’énergie. |
| d. | ↑ | Le temps caractéristique est défini comme le temps nécessaire pour que l’amplitude des oscillations de ξ soit multipliée par \(e\approx\) 2.718, mais pour faire simple, c’est juste le temps de destruction. |





