Tout le monde sait qu’un ordinateur a besoin d’électricité pour fonctionner, mais savez-vous de combien exactement ? Peut-on réduire sa consommation autant que l’on veut ou existe-t-il une quantité minimale d’énergie, est nécessaire pour manipuler de l’information ?
Le principe de Landauer, qui a été introduit en 1961 par Rolf Landauer [1], stipule que : « les opérations logiques irréversibles requièrent nécessairement la production d’une quantité minimale d’énergie, de \(k_\mathrm{B}T\,\mathrm{ln}(2)\) par bit manipulé » (où \(k_B\) est la constante de Boltzmann et \(T\) la température).
Pour comprendre ce que cela signifie, il faut d’abord comprendre de quoi il est question. Un « bit » désigne le plus petit système permettant de stocker de l’information. C’est-à-dire un système capable d’enregistrer une information qui peut prendre seulement deux valeurs, par exemple « vrai ou faux ». Les bits sont utilisés en informatique et sont les plus petits systèmes mémoire existants. Ils sont souvent représentés par les chiffres « 0 » et « 1 » (« 0 » pour « faux » et « 1 » pour « vrai »). Sur les CD par exemple, les données sont inscrites sous forme de creux (« 0 ») ou de plats (« 1 ») sur la surface du disque. Et pour lire l’information, on utilise un faisceau laser dont la réflexion sur le disque sera différente selon qu’il passe sur un creux ou un plat.
Une opération logique est une opération qui va manipuler des bits. Les opérations logiques prennent une entrée, et renvoient une sortie qui dépend de la valeur de l’entrée. L’entrée comme la sortie peuvent être composées d’un ou plusieurs bits. Par exemple, l’opération « ET » prend deux entrées a et b, et renvoie une sortie s. La sortie s est vraie (s=1) seulement si a et b sont vrais en même temps (c’est-à-dire si a=1 et b=1), et elle est fausse (s=0) dans les trois autres cas (voir la table logique ci-dessous).
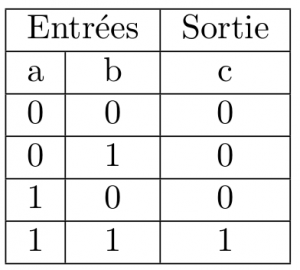
Une opération logique irréversible est une opération logique pour laquelle regarder la sortie ne permet pas toujours de déduire l’entrée. C’est le cas pour le « ET » logique, puisqu’il y a 4 entrées possibles, mais seulement deux sorties différentes. Par exemple, si on sait juste que s=0, on ne peut pas dire avec certitude ce que valaient a et b, car il y a 3 entrées différentes qui donnent cette même sortie. Le cas le plus simple d’opération logique irréversible est la « remise à zéro » : c’est l’opération pour laquelle il y a une seule entrée (qui peut donc valoir « 1 » ou « 0 ») et une seule sortie qui vaut toujours « 0 ».
Pour résumer : ce que dit le principe de Landauer, c’est qu’il y a une quantité d’énergie minimale qui doit être dissipée en chaleur pour chaque opération logique irréversible effectuée sur un système mémoire. Ce qui est important, c’est qu’il s’agit d’un principe fondamental qui ne suppose rien sur la nature du système mémoire utilisé. On peut d’ailleurs montrer que c’est en fait une reformulation du second principe de la thermodynamique, qui prédit que l’entropie d’un système isolé ne peut que croître (voir annexe pour la démonstration).
En revanche, la valeur de la quantité d’énergie dissipée est très faible, et les ordinateurs actuels fonctionnent avec un coût énergétique très supérieur à cette limite. En effet, la quantité \(k_\mathrm{B}T\,\mathrm{ln}(2)\) correspond environ à \(3\times10^{-21}\) joule à température ambiante (~25°C). En comparaison, l’énergie nécessaire pour augmenter de 1°C la température d’1 mL d’eau est de 4,18 joules, soit des milliards de milliards de fois plus ! Et les ordinateurs standards consomment environ 10-14 joule pour chaque opération effectuée sur un bit, soit plus d’un million de fois la valeur minimale théorique. Une question que l’on peut se poser est donc : « peut-on concevoir un système mémoire capable d’atteindre cette limite » ?
Au Laboratoire de Physique de l’ENS de Lyon, lors de ma thèse sous la direction de Sergio Ciliberto et Artem Petrosyan, nous avons justement réalisé une procédure expérimentale permettant d’atteindre la limite de Landauer [2] [3].
Pour cela nous avons dû travailler à l’échelle du micromètre (soit un millième de millimètre), où les quantités typiques d’énergie mises en jeu sont de l’ordre de l’énergie thermique : \(k_\mathrm{B}T\). Mais il faut savoir qu’à l’échelle micrométrique les objets ne sont jamais au repos, à cause de l’agitation thermique. En effet, un petit objet immergé dans un fluide est constamment bombardé par les molécules du fluide qui l’entourent, et il en résulte un déplacement aléatoire de l’objet : c’est le mouvement brownien. Ce phénomène est par exemple visible sur cette vidéo :

Une bille de silice (verre) de 2 µm de diamètre est plongée dans de l’eau à température ambiante, elle suit une trajectoire aléatoire (mouvement Brownien) à cause de l’agitation thermique.
Pour pouvoir faire un système mémoire à deux états, nous avons utilisé des pièges optiques. Les pièges optiques (parfois aussi appelés « pinces optiques ») sont des outils permettant de piéger et manipuler des petites particules (typiquement entre 100 nm et 10 µm) à l’aide d’un faisceau laser. On peut voir leur effet dans la vidéo suivante :

La même bille de silice que précédemment se déplace aléatoirement à cause du mouvement brownien, et le point lumineux correspond à un faisceau laser qui est focalisé à l’aide d’un objectif de microscope. Lorsque la bille passe à proximité de la tâche lumineuse, elle est attirée puis piégée. Elle ne peut alors s’en éloigner malgré l’agitation thermique. En revanche, lorsque le faisceau laser est éteint, la bille est libérée et reprend son déplacement aléatoire.
Pour créer un système mémoire à deux états, il suffit donc de placer deux pièges optiques côte à côte et d’y placer une bille. Il ne reste plus alors qu’à appeler « 0 » l’état où la bille est dans le puits de gauche, et « 1 » l’état où la bille est dans le puits de droite (voir figure 1).
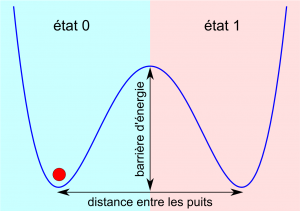
Afin de faire une procédure de « remise à zéro », nous avons rajouté une force qui pousse la bille vers le puits de gauche (numéroté « 0 »). Cette force est créée à l’aide d’un courant de fluide autour de la particule. La particule continue de se déplacer aléatoirement à cause de l’agitation thermique, mais de même qu’il est difficile de remonter une rivière à contre-courant, elle aura moins de chance d’aller dans le puits qui se trouve dans la direction opposée au courant.
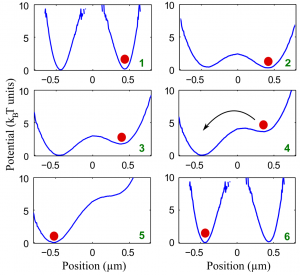
La procédure expérimentale est schématisée figure 2, et composée de plusieurs étapes :
- Initialement la particule est piégée dans l’un ou l’autre des deux puits ;
- on abaisse d’abord la barrière entre les deux puits pour faciliter le passage de l’un à l’autre ;
- à 5. on pousse progressivement la particule vers le puits souhaité à l’aide du courant d’eau ;
6. enfin on arrête de pousser et on remonte la barrière de potentiel pour séparer les deux puits.
Cette procédure est bien une procédure de remise à zéro, car la particule finit dans le puits de gauche, peu importe sa position initiale.
Nous avons ensuite mesuré la quantité d’énergie dissipée sous forme thermique (Q) par la particule lors de cette procédure. Pour cela, il faut connaître le déplacement de la particule, et la force qui s’applique sur elle. Heureusement, ces deux grandeurs sont accessibles expérimentalement : la trajectoire de la particule est mesurée directement à l’aide d’un microscope, et la force qui est appliquée par l’écoulement est connue et dépend seulement de sa vitesse, de la viscosité du fluide, et du rayon de la particule.
Bien évidemment, plus la force qui pousse la particule est grande, plus l’énergie dissipée est grande. Mais en contrepartie, plus la force est faible, plus il y a de risque que la bille n’aille pas dans la direction souhaitée. En effet, dans le cas limite où la force est nulle, la particule aura 50% de chance d’aller à gauche et 50% de chance d’aller à droite.
C’est pourquoi nous avons cherché à atteindre une procédure « optimale » à durée imposée. C’est-à-dire que nous fixons le temps \(\tau\) que nous voulons que la procédure dure, puis nous cherchons à trouver la force la plus faible qui garantit que la particule va bien dans le puits de gauche dans plus de 95% des cas (taux de réussite ≥ 95%).
Les résultats que nous avons obtenus sont présentés sur la figure 3. Pour les procédures de courte durée (≤ 15 s), l’énergie dissipée Q est toujours en moyenne bien supérieure à la limite de Landauer de \(k_\mathrm{B}T\,\mathrm{ln}(2)\). Lorsque la procédure devient de plus en plus lente, l’énergie dissipée diminue jusqu’à une valeur finie, en bon accord avec la limite théorique prédite par le principe de Landauer !
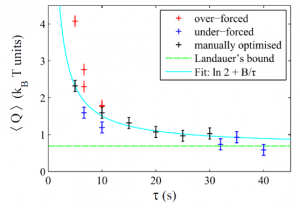
) en fonction de la durée de la procédure de remise à zéro (τ). Les points noirs correspondent aux procédures optimisées, les points bleus correspondent à des procédures sous-optimales qui ont un taux de réussite inférieur à 95%, et les points rouges correspondent à des procédures sur-optimales où la force est plus grande que nécessaire. La courbe bleue est un ajustement numérique fait sur les valeurs optimisées (points noirs).
Plus de 50 ans après la prédiction théorique de Landauer, nous avons donc réalisé une procédure expérimentale de « remise à zéro » d’un bit d’information, et nous avons vérifié que le coût énergétique associé à cette procédure, était toujours au moins égal à \(k_\mathrm{B}T\,\mathrm{ln}(2)\).
Certes, cette expérience est une expérience modèle, et elle ne correspond donc pas aux systèmes utilisés dans les vrais ordinateurs. De plus, l’utilisation d’un laser coûteux, et le temps nécessaire pour manipuler un seul bit (plusieurs secondes), ne la rendent absolument pas intéressante industriellement. Cependant elle permet néanmoins de faire un lien direct entre la thermodynamique et la théorie de l’information. En particulier, elle permet de comprendre pourquoi manipuler de l’information coûte toujours de l’énergie !
Même si les machines informatiques fonctionnent pour l’instant avec des coûts énergétiques bien plus élevés, l’existence d’une limite fondamentale se révélera peut-être importante à l’avenir, car cela signifie que leur consommation ne pourra pas être réduite autant qu’on pourrait le vouloir. Par ailleurs, la limite de Landauer ne s’applique pas qu’aux ordinateurs, mais a priori à tout système capable de manipuler de l’information, ce qui inclut donc la plupart des systèmes biologiques, comme par exemple tous les micro-organismes qui sont capables de mesurer et de répondre à une stimulation extérieure (lumineuse, chimique, etc.) !
Pour aller plus loin : Des informations supplémentaires et une discussion plus centrée sur la théorie de l’information peuvent être trouvée dans l’article « Information: From Maxwell’s demon to Landauer’s eraser » publié dans Physics Today [4].
Remerciements : Merci à Yannick et Sophie, et à l’équipe du Rayon, pour la relecture et les conseils !
Annexe : Lien entre le principe de Landauer et le second principe de la thermodynamique.
Le principe de Landauer est en fait une reformulation du second principe de la thermodynamique, appliqué à un système pouvant stocker de l’information.
En effet, si l’on considère un système à deux états (comme celui présenté figure 1), et que ce système est en équilibre avec un bain thermique qui impose une température T, alors il aura la même probabilité (50%) d’être dans l’un ou dans l’autre état. Dans ce cas, la formule de Boltzmann nous indique que son entropie vaut : \(k_\mathrm{B}\,\mathrm{ln}(\Omega)\) où \(\Omega\) désigne le nombre d’états de même probabilité qui sont accessibles au système, soit ici : \(\Omega=2\).
Si l’on fait maintenant subir au système une procédure de remise à zéro, le nombre d’états accessibles au système va être réduit à 1, et son entropie deviendra donc : \(k_\mathrm{B}\,\mathrm{ln}(1)=0\).
On voit donc qu’appliquer une procédure de remise à zéro à un système mémoire à deux états revient à diminuer son entropie d’une quantité égale à : \(k_\mathrm{B}\,\mathrm{ln}(2)\).
Or le second principe de la thermodynamique interdit que l’entropie d’un système isolé diminue. La perte d’entropie du système mémoire sera donc nécessairement compensée par une augmentation de l’entropie de l’extérieur. Cette augmentation d’entropie du bain thermique dans lequel est plongé le système mémoire sera payée sous forme de chaleur : \(Q>k_\mathrm{B}T\,\mathrm{ln}(2)\).









[…] Pourquoi manipuler de l’information coûte-t-il de l’énergie ? (SFP) […]