La physique quantique est une théorie qui complète la physique classique pour décrire notre monde aux petites dimensions. Elle permet ainsi de décrire comment un atome peut exister, et pourquoi un métal conduit l’électricité. Cependant, il est difficile de fabriquer des systèmes contrôlables et simples pour tester ses effets. Grâce à de nombreux progrès techniques depuis 30 ans, nous sommes capables de réaliser de plus en plus d’expériences, de mieux en mieux contrôléesa.
On peut, par exemple, piéger un (ou quelques) électrons à l’intérieur d’un circuit électrique aux dimensions microscopiques, puis étudier le comportement ondulatoire de l’électron ou sa superposition en deux états.
Dans cet article, je vous expliquerai tout d’abord comment piéger un électron dans un circuit électrique et les avantages d’un tel système. Je vous présenterai ensuite mon projet de thèse, et les résultats préliminaires obtenus.
Isoler un électron dans un circuit électrique : la boîte quantique
Lorsqu’on regarde un atome, ou plus précisément l’énergie d’un électron entourant le noyau, celle-ci ne peut pas prendre n’importe quelle valeur: elle est quantifiée. Par exemple, l’atome d’hydrogène H contient un électron, qui peut avoir pour énergie \( E_1= -13.6 eV\), b \( E_2= -3.4 eV\), \( E_3= -1.51 eV\)… Ou d’autres valeurs plus élevées.
Au laboratoire, on peut fabriquer un circuit électrique qui a la même propriété, c’est-à-dire dans lequel un seul, ou très peu de niveaux d’énergies sont accessibles aux électrons. De plus, deux électrons identiques ne peuvent pas se trouver dans un même niveau d’énergie (c’est le principe de Pauli): un tel circuit permet donc d’isoler un électron pour l’étudier. On l’appelle une boîte quantique.
Cependant, on ne peut pas fabriquer ce circuit avec n’importe quel matériau : à l’intérieur d’un bloc de métal, il y a de nombreux niveaux d’énergie disponibles, à des énergies très proches ! Il faut étudier un très petit morceau de conducteur électrique pour réduire le nombre de niveaux d’énergie, et les espacer: typiquement, toutes ses dimensions doivent être de l’ordre de 1 micromètre (ou moins) pour avoir des niveaux suffisamment séparés losque la température est de 1K (-272 °C). Ici, suffisamment séparés, veut dire que l’agitation thermique ne fournit pas une énergie suffisante pour qu’un électron puisse être transféré d’un niveau à un autre.
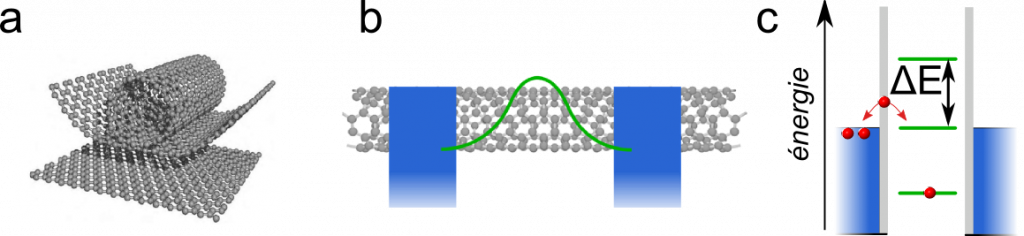
Pour former une boîte quantique, je commence donc par fabriquer, sur une puce de silicium, un nanotube de carbone. C’est un tube, formé d’une unique couche d’atomes de carbone enroulée sur elle-même, d’un diamètre de l’ordre du nanomètre (figure 1-a). Il »pousse » spontanément quand on chauffe du méthane en présence d’un peu de ferc. Je dépose ensuite deux électrodes métalliques sur une portion de un micromètre de ce nanotube (figure 1-b). À l’intérieur du segment de nanotube, les énergies accessibles aux électrons sont espacées de \(\Delta E\), comme représentées schématiquement sur la figure 1-c. Les électrodes métalliques ferment le circuit électrique et me permettent d’appliquer une tension et de mesurer le courant qui traverse le circuit. Ce courant permet de mesurer directement des niveaux d’énergie, comme expliqué sur la figure 2, quand les mesures sont effectuées à très basse température. Je place donc mon circuit dans un cryostat, un appareil qui permet d’isoler et maintenir un circuit à des températures de moins de 1K (jusqu’à 20 mK)d.
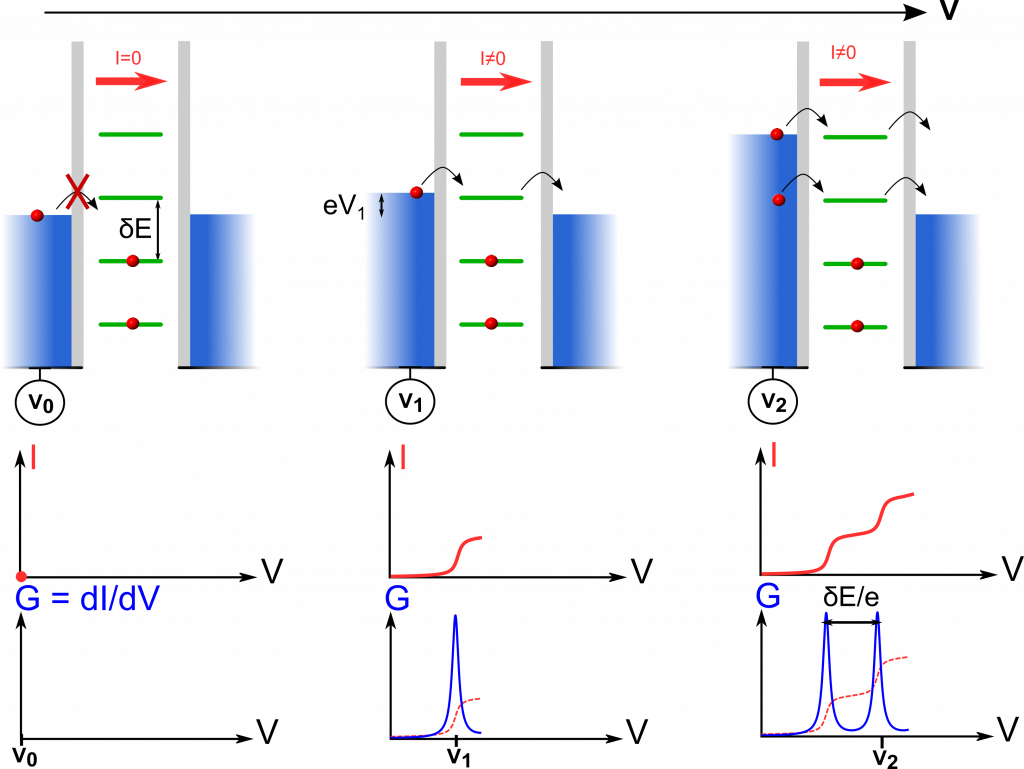
Sur certains schémas, les électrons sont représentés comme des boules rouges par soucis de simplicité. Cependant, il faudrait plutôt les représenter comme une onde se propageant et faisant des aller-retours dans le segment de nanotube, se reflétant à chaque bout, telle de la lumière entre deux miroirs ou une vibration dans une corde à sauter. Les ondes allers et retours se superposent, et au final l’électron est mieux représenté par sa `’fonction d’onde », un fonction qui représente la probabilité d’observer l’électron à une certain position du nanotube. C’est cette fonction d’onde qui est représentée figure 1-b).
Un électron partagé…
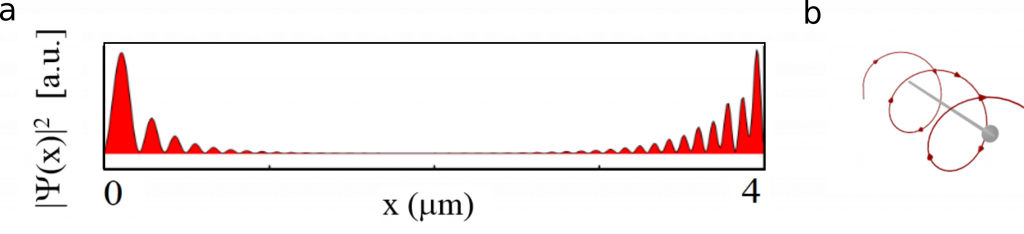
Mon projet de thèse consiste à modifier la forme de cette fonction d’onde dans l’espace, soit en quelque sorte la « forme » de l’électron piégé.
La forme d’une onde électronique dans une boîte quantique est typiquement une sinusoïde (comme par exemple dans la figure 1-b), mais elle peut changer si l’électron est soumis à certains effets physiques, jusqu’à ce que le nouvel état du système prenne la forme de la figure 3-a où on voit une quasiparticule qui semble séparée en deux. C’est cette forme que j’essaye d’obtenir, car chaque moitié de la quasiparticule a des propriétés différentes de celles d’un quasiélectron seule.
Pour arriver à déformer l’électron de cette manière, il faut regrouper dans la boîte quantique trois effets physiques qui agissent sur le spin de l’électron, et n’ont pas l’habitude de cohabiter : de la supraconductivité, un champ magnétique et du couplage spin-orbite.
Expliquer ces différents effets et leur lien avec l’électron déformé de manière rigoureuse est compliqué, et ce n’est pas le cœur de l’expérience que j’ai réalisé. En une phrase, en combinant ces effets on réalise une compétition entre deux manières de former des paires d’électrons. On peut faire en sorte que le long du nanotube, il y ait deux régions, où deux façons différentes de créer des paires d’électrons prédominent : une région où les paires de type 1 ont une énergie plus faible, et une où ce sont les paires de type 2f. À l’interface entre ces deux régions, les deux type de paires ont la même énergie, et une quasiparticule existe à énergie nulle.
Ces quasiparticules particulières attirent l’intérêt des théoriciens qui réfléchissent à la fabrication d’ordinateurs quantiques. Par ordinateur quantique, on veut dire un outil de calcul qui fonctionnerait de manière très différente de nos ordinateurs classiques, à l’aide de nouveaux algorithmes fondés sur l’utilisation de qubit, analogue des bits classiques dans nos ordinateurs. Le demi-électron permettrait de former de tels qubit g. Cependant, l’ordinateur quantique est encore un débouché très long terme, qui nécessite de lever encore de nombreux verrous techniques avant de pouvoir – peut-être – voir le jour. Heureusement, la recherche dans ce domaine ouvrira sûrement la voie à de nombreuses autres applications !
Je vais maintenant vous parler plus en détails de la première étape de mon projet, qui fut d’ajouter à ma boîte quantique un couplage spin-orbite. De manière très générale, on appelle couplage spin-orbite un effet physique qui modifie l’énergie d’un électron en fonction de son spin et de son mouvement, comme le ferait une force qui fait tourner le spin de l’électron lorsqu’il se déplace, comme représenté figure 3-b. Ce couplage est une propriété intrinsèque à certains matériaux, mais il est souvent très faible, notamment dans le nanotube de carbone qui me sert de circuit. Il a donc fallu trouver un moyen de le synthétiser, c’est-à-dire générer une force qui puisse relier le spin de l’électron avec son déplacement. C’est l’étape la plus compliquée et nouvelle de mon projet; les deux ingrédients restants, supraconductivité et magnétisme, ont déjà été ajoutés à des circuits semblables aux miens1.
Synthétiser un couplage spin-orbite
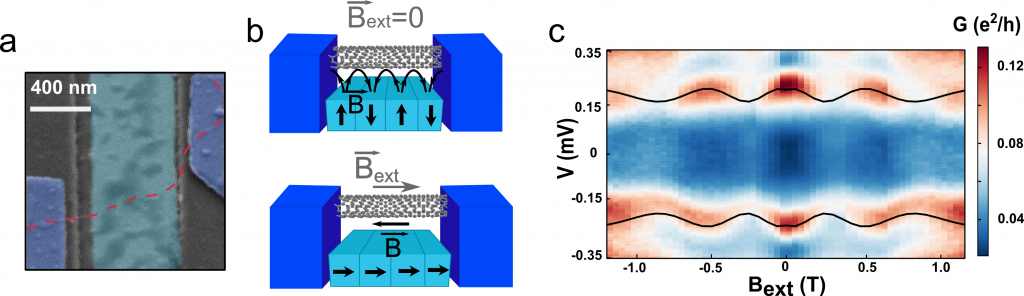
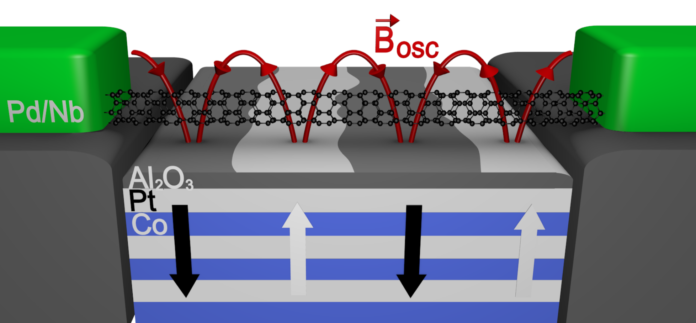
b) Représentation schématique du circuit électrique dans deux situations. En haut, sans champ magnétique extérieur. Le métal ferromagnétique présente des domaines d’aimantation (en noir) qui créent un champ magnétique qui oscille dans l’espace. En bas, un champ magnétique extérieur est appliqué (gris), et aligne les domaines dans son axe: le champ au niveau du nanotube est homogène (noir). c) Evolution d’un niveau d’énergie de la boîte quantique en fonction du champ magnétique extérieur, observé à travers une mesure de conductance électrique en fonction de la tension appliquée aux bornes de la boîte quantique et du champ magnétique extérieur (voir figure 2 pour le principe de la mesure électrique). La dépendance des niveaux en fonction du champ exterieur montre indirectement l’effet du champ magnétique créé par le métal ferromagnétique sur l’électron piégé.
La solution que j’ai mise en oeuvre fut de placer le circuit électrique au dessus d’un matériau qui contient des domaines d’aimantations opposés comme représenté figure 4-a et b; autrement dit, ce matériau agit comme une succession d’aimants d’orientations opposées (les flèches noires de la figure 4-b). Ces aimants créent un champ magnétique qui oriente le spin de l’électron dans l’axe du champ, et cet axe évolue le long de la trajectoire de l’électron (en rouge sur la figure 3-a): ils imitent donc bien un couplage spin-orbite 2.
Pour réussir à avoir un couplage suffisamment fort, j’ai collaboré avec des chercheurs du LPS qui travaillent sur le magnétisme pour répondre au cahier des charges suivant: obtenir des aimants très petits (de l’ordre de 100nm), qui génèrent un champ magnétique fort, et dont la préparation est compatible avec le reste du processus de fabrication du circuit.
Reste enfin à observer l’effet : dans mon expérience, je mesure les niveaux d’énergie de la boîte quantique. Or, ceux-ci évoluent périodiquement avec la force du couplage spin-obite synthétiqueh. En appliquant un champ magnétique uniforme dans l’espace, on peut petit à petit aligner les aimants et atténuer la force du couplage, ce qui fait osciller l’énergie de l’électron. C’est ce que nous montre la figure 4-c, où les lignes rouges correspondent à l’énergie de l’électron piégé.
Ce travail a été publié ici à la fin de ma thèse3. La réalisation expérimentale d’un couplage spin-orbite synthétique ouvre des applications non seulement dans le domaine de l’information quantique avec la recherche des demi-électrons dont je vous ai parlé au paragraphe 2, mais aussi dans d’autres domaines qui cherchent à utiliser le spin de l’électron, par exemple pour stocker de l’information (électronique de spin).
Pour aller plus loin: Un système très modulable
Avoir isolé un électron dans un circuit électrique sur puce de silicium présente plusieurs avantages. D’une part, on a tous les outils de l’électronique classique à notre disposition pour l’étudier (ils nous ont aussi aidé à fabriquer un tel circuit!). D’autre part, il est facilement manipulable, par exemple pour le placer à l’intérieur d’un champ magnétique ou l’illuminer à l’aide d’un laser (voir l’article de Adrien Jeantet). Finalement, on peut contrôler certaines grandeurs physiques, simplement en modifiant le circuit : espacement des niveaux d’énergie, interactions entre électronsi…
En allant plus loin, on peut même utiliser cette modularité pour obtenir de nouveaux états quantiques, qui peuvent avoir des propriétés différentes de celles d’un électron isolé :
- En plaçant le circuit proche d’un photon (piégé dans une cavité par exemple), l’interaction de la charge de l’électron avec le champ électromagnétique du photon, si elle est suffisamment forte, transforme l’état de l’électron piégé. Il peut être intriqué avec le photon, c’est-à-dire qu’on ne peut plus définir un état distinct pour l’un ou pour l’autre, mais un état mixte ; en conséquence la vitesse de propagation ou encore la masse de cet état sont différents de celui du quasiélectron isolé4.
- En utilisant des métaux particuliers pour les électrodes, on peut modifier l’interaction entre notre électron et son environnement. Une électrode aimantée agit sur son spin ; une électrode supraconductrice permet de former, dans le circuit, des paires d’électrons1.
1.Pillet J-D, Quay CHL, Morfin P, Bena C, Yeyati AL, Joyez P. Andreev bound states in supercurrent-carrying carbon nanotubes revealed. N. 2010;6(12):965-969. doi:10.1038/nphys18112.Egger R, Flensberg K. Emerging Dirac and Majorana fermions for carbon nanotubes with proximity-induced pairing and spiral magnetic field. P. 2012;85(23). doi:10.1103/physrevb.85.2354623.Desjardins MM, Contamin LC, Delbecq MR, et al. Synthetic spin–orbit interaction for Majorana devices. N. 2019;18(10):1060-1064. doi:10.1038/s41563-019-0457-64.Mi X, Cady JV, Zajac DM, Deelman PW, Petta JR. Strong coupling of a single electron in silicon to a microwave photon. S. 2016;355(6321):156-158. doi:10.1126/science.aal2469
Notes
| a. | ↑ | pour un bref aperçu, voir http://rapports-du-comite-national.cnrs.fr/rapport-conjoncture/rapport-de-conjoncture-2014/ii-physique-mesoscopique |
| b. | ↑ | c’est une unité d’énergie (pour parler d’effets microscopiques, elle est plus adaptée que les Joules ou les kcal). |
| c. | ↑ | De manière simplifiée, le tube commence à se former autour d’un grain de catalyseur (fer) puis s’allonge |
| d. | ↑ | Pour avoir une idée de ce à quoi cela ressemble. |
| e. | ↑ | C’est une quasiparticule qui est sa propre anti-quasiparticule; on appelle de telle particules des fermions de Majorana |
| f. | ↑ | Ces deux type de paires correspondent à différentes orientations des spins des électrons |
| g. | ↑ | Pour aller plus loin, voir « An Introduction to Quantum Computing » par Phillip Kaye, Raymond Laflamme, Michele Mosca |
| h. | ↑ | Via la relation de dispersion, qui lie l’énergie de l’électron et la période de l’onde électronique, ainsi que les conditions aux limites qui décrivent le piégeage de l’électron |
| i. | ↑ | qui sont des constantes dans le cas des électrons d’un atome isolé – un des systèmes d’étude alternatif possible |









J’ai beaucoup aimé votre présentation dans son ensemble. Mais quelques détails me chiffonnent.
Le clic sur les références des notes a et d renvoient l’erreur 404 (la cible n’existe pas).
Je ne sais pas interpréter ‘image a de la fig. 4 et le texte qui la commente ne m’aide pas.
Je vois croit tout à fait quand vous dites que « les différents effets et leur lien avec l’électron déformé de manière rigoureuse est compliqué ». C’est là que je souhaiterais en savoir plus !
Maintenant je me présente : Denis Chadebec, P.R.A.G (qui a exercé en lycée en province) en retraite depuis 2009, assidu aux congrès de la S.F.P et de l’U.d.P.P.C. Le site référé propose des pages de ressources pédagogiques en libre service pour quiconque cherche à communiquer de la physique (voire des mathématiques) au public le plus large avec des arguments solides.
Encore bravo pour cette production !
Et pardon pour quelques fautes de français (l’image a de la fig. 4, je vous crois,