Tourbillons quantiques et oscillations de densité dans un condensat fermionique

Les calculs numériques créent souvent un pont entre la physique théorique et expérimentale. Aujourd’hui, je vais vous raconter mes simulations de gaz atomiques ultra-froids. Nous verrons que des vortex quantiques peuvent coexister avec des phénomènes éphémères. Ces phénomènes attendent encore une confirmation expérimentale, mais ils enflamment déjà l’esprit des scientifiques.

Je suis sûr que vous savez bien ce qu’est un atome. Les différents atomes ont des tailles et masses différentes, certains forment des molécules facilement et d’autres ne sont pas tellement réactifs. Il est possible de classifier les atomes en fonction de leurs propriétés. Par exemple, ils peuvent être classés de deux manières selon leur spin (moment magnétique interne) : fermions ayant un spin demi-entier (½, 3/2, 5/2…) et bosons ayant un spin entier (0, 1, 2…). La valeur du spin est importante, mais il faut savoir que le spin est un vecteur. Si vous pensez à un atome traversé par une flèche, vous avez plus ou moins une bonne image dans votre tête. D’ailleurs, les signes “plus” et “moins” sont utilisés pour montrer le sens du spin. “Plus” pour le spin orienté vers le haut spin up et “moins” pour le sens opposé spin down. Imaginons maintenant que nous ayons un gaz d’atomes. Il s’avère que les propriétés de ce gaz sont différentes selon le genre d’atomes que nous utilisons.

En refroidissant un gaz de bosons jusqu’à une température extrêmement proche du zéro absolu, c’est-à-dire presque -273,15 ℃ (c’est un gaz quantique ultra-froid), on observe que le nuage d’atomes devient de plus en plus petit. Pourtant, la même observation n’accompagne pas une expérience analogue avec des fermions. Pourquoi ? Car les bosons obéissent à une statistique quantique différente de celle des fermions. Cela permet de serrer les bosons dans un petit volume. Pour être précis, dans une telle situation presque tous les bosons occupent l’état fondamental, c’est-à-dire leur état de plus basse énergie. Ce phénomène est appelé la condensation de Bose-Einstein. Dans un tel condensat, les bosons peuvent se déplacer sans viscosité. Une fois ce gaz mis en mouvement, il ne cessera jamais de couler. On appelle cela la superfluidité.

En revanche, la statistique de Fermi-Dirac, qui est celle associée aux fermions, interdit à deux fermions identiques de se loger sur le même niveau d’énergie. Pour autant, cela ne rend pas la condensation de gaz de fermions impossible. Néanmoins, le mécanisme qui l’explique est un peu plus compliqué. Ce mécanisme a été décrit par John Bardeen, Leon Cooper et Robert Schrieffer en 1957 (tous les trois ont reçu le prix Nobel 15 ans plus tard) ^​1,2​ : deux  fermions de spins opposés (spin up et spin down qui ont par exemple un spin +½ et -½ ) créent une paire de Cooper. Chaque paire possède un spin entier. Cela nous permet de les traiter comme des bosons. Cette explication nous suffit pour que vous compreniez ce qui se passe avec des fermions pendant leur refroidissement. 

Le gaz est très souvent confiné avec un potentiel harmonique. Utilisons une métaphore : ce potentiel est comme une tasse qui garde le gaz à l’intérieur. Si on a déjà un gaz de fermions ultra-froid, on peut utiliser un laser – comme une cuillère – pour le remuer. Et voilà comment on produit des tourbillons appelés vortex quantiques^​3,4​. Ces vortex ont un diamètre caractérisé par la longueur de cohérence \( \xi \). On utilise les vortex comme indicateurs de la superfluidité. 

Nous pouvons nous interroger sur le nombre de vortex dans notre système. Est-ce que l’on obtiendra \( n \) petits vortex ou un vortex géant ? Dans ce premier cas, l’énergie du système est égale à \( nE\) (où \( E \) est l’énergie d’un seul petit vortex). Pourtant, s’il y avait un seul vortex, cette énergie serait \( n \) fois plus grande ^a, c’est-à-dire \( n^2 E \). On dit alors qu’il est énergétiquement plus favorable de produire plusieurs vortex qu’un seul vortex géant. 

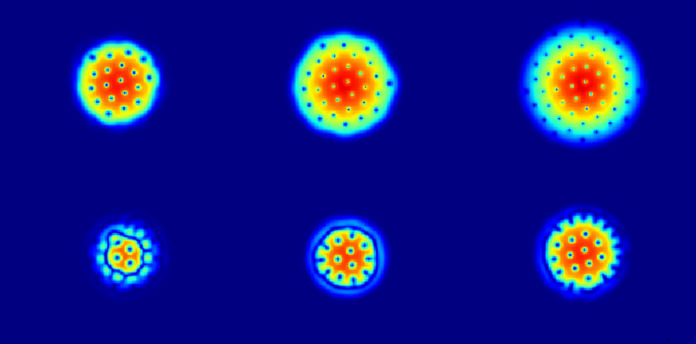
On observe de nombreux vortex dans notre gaz. Ils forment une structure régulière. On connaît les détails de réseaux de vortex grâce à Alexeï Abrikossov, le lauréat du prix Nobel de 2003 ^​1,2,5​. Nota bene, il avait affirmé que ces réseaux étaient carrés. Cependant les vortex forment des triangles (voir figure 1). Cette petite erreur n’a quand même pas drastiquement influencé l’estime pour sa découverte.

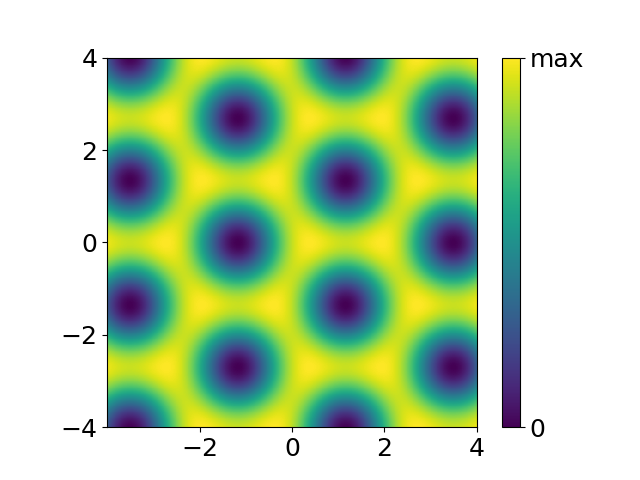
L’observation du gaz ultra-froid en rotation est une méthode pour distinguer la phase superfluide, avec des paires de Cooper, de la phase normale qui est constituée d’atomes en excès. Le superfluide ne manifeste la rotation que par la création des vortex. Cette contrainte ne s’applique pas à la phase normale. Elle répond à la rotation par une simple circulation, juste comme un thé lentement remué. En bref, si l’on voit des vortex, c’est la phase superfluide. Sinon, on observe la phase normale.

Maintenant nous sommes face à la plus importante question de ce texte. Que se passe-t-il avec ce réseau quand le nombre d’atomes spin up et spin down est différent ? Ici, il faut que l’on jette un coup d’œil sur un paramètre qui nous indique quelle est la différence de densité entre atome de spins up ou down. On l’appelle polarisation. Si la valeur de la polarisation est 0, il y a autant d’atomes spin up que spin down. Si la polarisation est égale à 100%, cela veut dire que nous n’avons que les atomes spin up. Imaginez une situation où le système est polarisé (c’est-à-dire si la polarisation n’est pas de 0 %). Certains atomes cherchent et trouvent les autres qui leur manquent tant pour créer des paires de Cooper. Ceux qui ne sont pas capables de le faire restent sans leur partenaire particulier.

Le premier pas pour trouver la réponse à notre question c’est d’établir un modèle théorique. Le dernier pas sera de préparer une expérience. En effet, il est toujours utile pour les expérimentalistes de savoir ce qu’ils doivent chercher. Et le modèle théorique qu’on utilise ici est assez complexe. On ne peut pas résoudre ce type d’équations ni analytiquement, ni avec un ordinateur ordinaire. La seule solution est d’utiliser un superordinateur qui est capable de faire ce calcul !

Cela a été un immense plaisir de faire partie du groupe de l’École polytechnique de Varsovie. Nous avons élaboré des simulations numériques et je vais vous expliquer nos principaux résultats dans la suite de cet article.

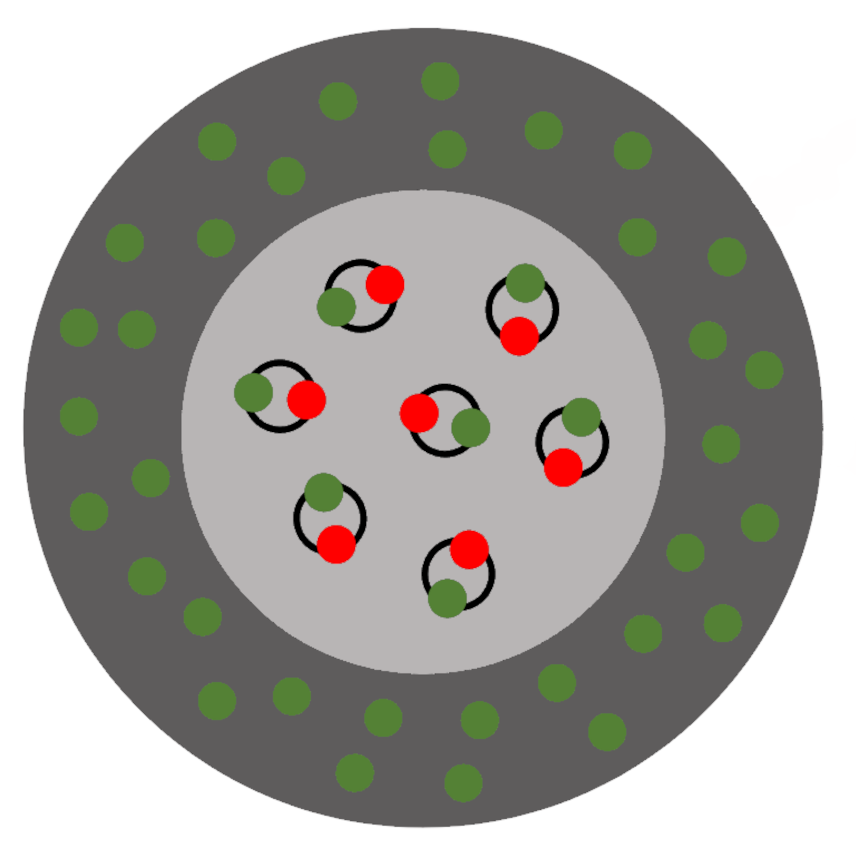
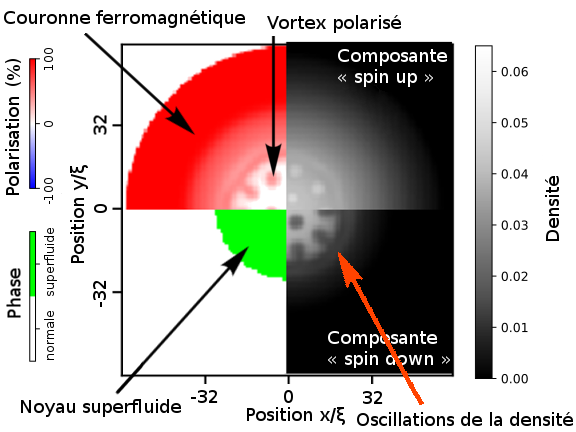
Premièrement, les simulations nous montrent que le système polarisé se sépare en un noyau qui est superfluide et une couronne qui est ferromagnétique (voir le schéma de la figure 2 et la partie gauche de la figure 3 ^​6​). On appelle cette dernière de cette façon, car ses spins sont alignés spontanément dans la même direction, exactement comme dans un magnet. Si cette polarisation globale augmente, le noyau superfluide rétrécit, jusqu’à la polarisation globale critique (environ 75 % ^​4​) où la superfluidité disparaît totalement. Au-dessus de cette polarisation globale, on ne voit plus de vortex.

Un autre phénomène, qui attire beaucoup l’attention, est la formation de la phase exotique du type Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) ^​7,8​. Elle apparaît sur l’interface entre le noyau superfluide et la couronne ferromagnétique. Cette phase est visible en raison d’oscillations de la densité qui se forment dans ce système (voir la flèche orange sur figure 3). L’anneau gris pâle sur la figure 3 correspond à une concentration élevée d’atomes. Notez que la hausse dans la densité d’un composant est liée à la baisse de densité de l’autre, illustrée par un anneau gris foncé. Quand on sort du noyau superfluide vers la couronne, la densité oscille. On y voit une baisse, puis la densité augmente et baisse encore une fois. Il est très difficile de détecter ces oscillations. En dépit du fait que la phase FFLO ait été postulée en 1964, elle n’a pas encore été trouvée expérimentalement dans les gaz atomiques.

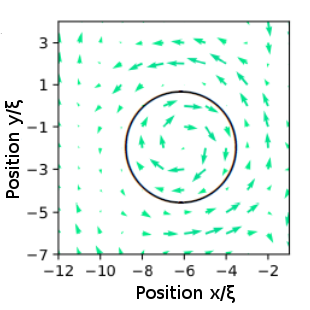
De plus, on peut remarquer que l’espace vide dans les vortex est occupé par les atomes excessifs (c’est-à-dire polarisé). Ces atomes tournent dans le sens opposé à la partie superfluide. On dit que le flux à l’intérieur est inversé (voir figure 4). Une analyse détaillée de ce phénomène nous donne une explication sur le fait qu’ils circulent dans un sens opposé aux autres. En bref, dans le système non-polarisé, les atomes ne peuvent qu’occuper les états quantiques qui correspondent à la rotation dans un sens (disons horaire). Dès qu’une polarisation suffisante apparaît, on voit un changement drastique dans le paysage énergétique. Les états qui correspondent à la rotation dans le sens horaire, deviennent accessibles aux atomes excessifs et on observe le flux inversé^​9​.

En conclusion, il était prédit que les gaz de fermions peuvent former des structures très intéressantes avec la séparation de phase et des apparitions de petits vortex. Ces deux phénomènes ont été déjà observés expérimentalement avec de vraies particules ^​4​. Mais il y a plus à découvrir. Mes collègues et moi avons simulé numériquement des particules qui révèlent des effets encore plus exotiques que ceux-là, comme la présence de la phase exotique FFLO et du flux inversé ! Les simulations peuvent maintenant donner de bons paramètres à explorer pour les prochaines équipes de chercheur.e.s qui voudront tenter d’observer ces phénomènes. Le reste n’est pas silence mais appartient aux expérimentateur.rice.s.